
分析 先把分子分母因式分解和除法运算化为乘法运算,再约分得到原式=$\frac{x+6}{x+1}$,然后利用x+1与x+6互为相反数可得到原式的值.
解答 解:原式=$\frac{x}{x+3}$•$\frac{(x+3)^{2}}{x(x+1)}$+$\frac{3(x-1)}{(x+1)(x-1)}$
=$\frac{x+3}{x+1}$+$\frac{3}{x+1}$
=$\frac{x+6}{x+1}$,
∵x+1与x+6互为相反数,
∴原式=-1.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.


科目:初中数学 来源: 题型:选择题
 如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=$\sqrt{6}$,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=( )
如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=$\sqrt{6}$,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0≤m≤1 | B. | -3≤m≤1 | C. | -3≤m≤3 | D. | -1≤m≤0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
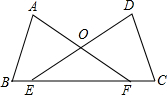 如图,点B、E、F、C在同一直线上,点A、D位于BC同侧,AB=DC,BE=CF,∠B=∠C.
如图,点B、E、F、C在同一直线上,点A、D位于BC同侧,AB=DC,BE=CF,∠B=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A(0,2),B(2,2),C(-1,-2),抛物线F:y=x2-2mx+m2-2与直线x=-2交于点P.
如图,已知点A(0,2),B(2,2),C(-1,-2),抛物线F:y=x2-2mx+m2-2与直线x=-2交于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com