
分析 (1)根据幂的乘方、有理数的乘法和减法可以解答本题;
(2)根据幂的乘方、有理数的乘法和减法可以解答本题;
(3)根据幂的乘方、有理数的乘法、除法和加法可以解答本题;
(4)根据幂的乘方、有理数的除法和减法可以解答本题.
解答 解:(1)(-$\frac{1}{3}$)×(-3)3-0.25×(-3)×(-2)4
=$(-\frac{1}{3})×(-27)-0.25×(-3)×16$
=9+12
=21;
(2)18+32-(-2)3-(-4)2×5
=18+32-(-8)-16×5
=18+32+8-80
=-32;
(3)[(-5)2×(-$\frac{3}{5}$)+15]×(-2)3÷7
=[25×(-$\frac{3}{5}$)+15]×(-8)×$\frac{1}{7}$
=[-15+15]×(-8)×$\frac{1}{7}$
=0×(-8)×$\frac{1}{7}$
=0;
(4)($\frac{4}{3}$-$\frac{7}{6}$)2÷($\frac{1}{3}$-$\frac{1}{2}$)2÷(-$\frac{1}{6}$)2×(-$\frac{1}{2}$)3
=$(\frac{1}{6})^{2}÷(-\frac{1}{6})^{2}÷\frac{1}{36}×(-\frac{1}{8})$
=$\frac{1}{36}×36×36×(-\frac{1}{8})$
=-$\frac{9}{2}$.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 根据下面给出的数轴,解答下面的问题:
根据下面给出的数轴,解答下面的问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线CD与直线AB相交于C,根据下列语句画图
如图,直线CD与直线AB相交于C,根据下列语句画图查看答案和解析>>
科目:初中数学 来源: 题型:解答题
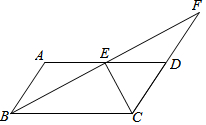 如图,在四边形ABCD中,AB∥CD,AD∥BC,AB=CD,AD=BC,点E是AD的中点,连接BE并延长交CD的延长线于点F.
如图,在四边形ABCD中,AB∥CD,AD∥BC,AB=CD,AD=BC,点E是AD的中点,连接BE并延长交CD的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com