Question

18．已知正方形ABCD，点E在直线CD上．
（1）若F是直线BC上一点，且AF⊥AE，求证：AF=AE；（请利用图1所给的图形加以证明）
（2）写出（1）中命题的逆命题，并画出一个图形说明该逆命题是假命题；
（3）若点G在直线BC上，且AG平分∠BAE，探索线段BG、DE、AE之间的数量关系，并说明理由．

Answer 1

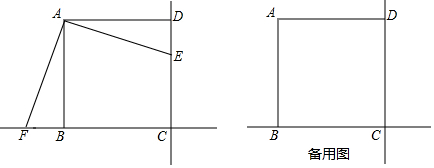
分析 （1）如图1，利用ASA证明△ABF≌△ADE，可以直接得出AE=AF；
（2）如图2所示，如果AF=AE时，AE与AF不一定垂直；
（3）分三种情况：
①当E在线段CD上时，满足AE=BG+DE，如图3，作辅助线，利用（1）的结论得：△ABF≌△ADE，得AE=AF，DE=BF，再证明AF=FG，利用等量代换和线段的和得出结论．
②当E在CD的延长线上时，满足BG=DE+AE，③当E在DC的延长线上时，满足AE=DE+BG；同理分别得出相应结论．

解答 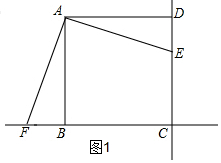证明：（1）如图1，∵四边形ABCD是正方形，
∴AB=AD，∠ABC=∠ADC=∠BAD=90°，
∴∠ABF=∠ADC=90°，∠DAE+∠BAE=90°，
∵AE⊥AF，
∴∠EAF=90°，
∴∠FAB+∠BAE=90°，
∴∠DAE=∠BAF，
∴△ABF≌△ADE，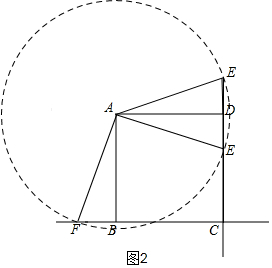
∴AE=AF；
（2）若F是直线BC上一点，且AF=AE，则AF⊥AE；
如图2所示，当AF=AE时，则AF与AE不一定垂直，所以“若F是直线BC上一点，且AF=AE，则AF⊥AE“是假命题；
（3）分三种情况：
①当E在线段CD上时，满足AE=BG+DE，理由是：
如图3，过A作AF⊥AE，与直线CB交于点F，
由（1）得：△ABF≌△ADE，
∴AE=AF，DE=BF，
∴FG=BF+BG=BG+DE，
∵AG平分∠BAE，
∴∠BAG=∠EAG，
∵∠BAF=∠DAE，
∴∠BAF+∠BAG=∠EAG+∠DAE，
∴∠FAG=∠DAG，
∵AD∥BC，
∴∠DAG=∠AGF，
∴∠AGF=∠FAG，
∴AF=FG，
∴AE=FG=BG+DE．
②当E在CD的延长线上时，满足BG=DE+AE，理由是：
如图4，
过A作AF⊥AE，与直线CB交于点F，
由（1）得：△ABF≌△ADE，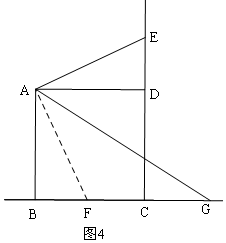
∴AE=AF，DE=BF，∠BAF=∠DAE，
∵AG平分∠BAE，
∴∠BAG=∠EAG，
∴∠BAG-∠BAF=∠EAG-∠DAE，
∴∠FAG=∠GAD，
∵AD∥BC，
∴∠DAG=∠AGF，
∴∠AGF=∠FAG，
∴AF=FG，
∴AE=FG=AF，
∴BG=BF+FG=DE+AE；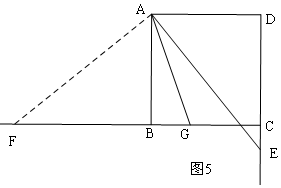
③当E在DC的延长线上时，满足AE=DE+BG，理由是：
如图5，过A作AF⊥AE，与直线CB交于点F，
同理得：△ABF≌△ADE，
∴AE=AF，DE=BF，
∴FG=BF+BG=BG+DE，
∵AG平分∠BAE，
∴∠BAG=∠EAG，
∵∠BAF=∠DAE，
∴∠BAF+∠BAG=∠EAG+∠DAE
∴∠FAG=∠DAG，
∵AD∥BC，
∴∠DAG=∠AGF，
∴∠AGF=∠FAG，
∴AF=FG，
∴AE=FG=BG+DE．

点评 本题是四边形的综合题，考查了正方形、全等三角形的性质和判定；正方形的各边相等且每个角都等于90°，在全等的证明中常利用同角的余角相等证明两个角相等，这一方法要熟练掌握；对于第三问中线段的和差问题，常利用全等三角形对应边相等作等量代换，得出结论．