
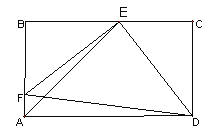
【题目】已知:如图,在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED, EF⊥ED.求证: AE平分∠BAD.
 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价![]() 元,乒乓球每盒定价
元,乒乓球每盒定价![]() 元,现两家商店搞促销活动,甲店:每买一副乒乓球拍赠送一盒乒乓球;乙店:按定价的九折优惠.某人需购球拍
元,现两家商店搞促销活动,甲店:每买一副乒乓球拍赠送一盒乒乓球;乙店:按定价的九折优惠.某人需购球拍![]() 副,乒乓球若干盒(不少于
副,乒乓球若干盒(不少于![]() 盒).
盒).
(![]() )设购买乒乓球盒数为
)设购买乒乓球盒数为![]() (盒),在甲商店付款为
(盒),在甲商店付款为![]() (元),在乙商店付款为
(元),在乙商店付款为![]() (元),分别写出
(元),分别写出![]() ,
, ![]() 与
与![]() 的关系式.
的关系式.
(![]() )就乒乓球盒数讨论去哪家商店买更优惠.
)就乒乓球盒数讨论去哪家商店买更优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)
(1)若已知CD=20米,求建筑物BC的高度;(2)若已知旗杆的高度AB=5米,求建筑物BC的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程2y2﹣7=3y的二次项系数、一次项系数、常数项分别是( )
A.2,﹣3,﹣7B.﹣2,﹣3,﹣7C.2,﹣7,3D.﹣2,﹣3,7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC、△DCE均为等边三角形,且B、C、E三点在一条直线上,BD与AE相交于O点.
(1)求证:△BCD≌△ACE;
(2)求∠DOE的度数;
(3)连接MN,求证:MN∥BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山东潍坊第23题)旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com