
【题目】已知,△ABC、△DCE均为等边三角形,且B、C、E三点在一条直线上,BD与AE相交于O点.
(1)求证:△BCD≌△ACE;
(2)求∠DOE的度数;
(3)连接MN,求证:MN∥BE.

【答案】见解析
【解析】试题分析:
(1) △ABC、△DCE均为等边三角形,易知BC=AC,CD=CE. 这样,对于△BCD与△ACE而言,已经获得了两组对应边的相等关系,只要再证明这两组对应边所夹的角∠BCD与∠ACE对应相等就可以用SAS证明这组三角形全等了.观察图形可知,∠BCD与∠ACE均是由等边三角形的一个内角加上一个相同的角∠ACD而形成的,进而可以证明其相等.
(2) 观察图形可知,∠DOE是△BOE的一个外角,容易联想到用三角形外角的相关结论求解该题. 利用三角形外角的相关结论以及第(1)小题中的全等三角形,可以将∠DOE转化为∠DBC+∠BDC,再由三角形外角的相关结论可知∠DOE与等边三角形内角∠DCE相等,得到答案.
(3) 分析条件可知∠ACN=60°,结合图形的形状可以猜想△MCN为等边三角形. 若△MCN为等边三角形,即可通过“内错角相等,两直线平行”的方法证明MN∥BE. 本题的问题转化为如何证明△MCN为等边三角形. 利用第(1)小题中的全等三角形可以证明△CAN与△CBM全等,得到CN=CM. 这样就证明了△MCN为等边三角形,进而容易证明MN∥BE.
试题解析:
(1) ∵△ABC与△DCE均为等边三角形,
∴BC=AC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠ACD =∠DCE+∠ACD,即∠BCD=∠ACE,
∵在△BCD与△ACE中:
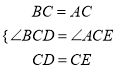 ,
,
∴△BCD≌△ACE (SAS).
(2) ∵∠DOE是△BOE的一个外角,
∴∠DOE=∠OBE+∠OEB,即∠DOE=∠DBC+∠AEC,
∵△BCD≌△ACE,
∴∠BDC=∠AEC,
∴∠DOE=∠DBC+∠BDC,
∵∠DCE是△BCD的一个外角,
∴∠DCE=∠DBC+∠BDC,
∴∠DOE=∠DCE,
∵△DCE为等边三角形,
∴∠DCE=60°,
∴∠DOE=∠DCE=60°.
(3) ∵△ABC与△DCE均为等边三角形,
∴AC=BC,∠ACB=∠DCE=60°,即∠BCM=∠ECN=60°,
∵B、C、E三点在一条直线上,
∴∠ACN+∠BCM+∠ECN=180°,
∴∠ACN=180°-∠BCM-∠ECN=180°-60°-60°=60°,
∴∠ACN=∠BCM,
∵△BCD≌△ACE,
∴∠CBD=∠CAE,即∠CAN=∠CBM,
∵在△CAN与△CBM中:
 ,
,
∴△CAN≌△CBM (ASA),
∴CN=CM,
∵∠ACN=60°且CN=CM,
∴△MCN为等边三角形,
∴∠CMN=60°,
∴∠CMN=∠ACB=60°,
∴MN∥BE.


科目:初中数学 来源: 题型:
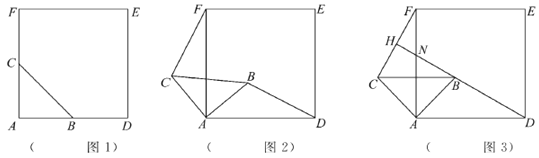
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3时,求线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青藏高原是世界上海拔最高的高原,它的面积约为2500000平方千米.将2500000用科学记数法表示应为( )
A.0.25×107
B.2.5×107
C.2.5×106
D.25×105
查看答案和解析>>
科目:初中数学 来源: 题型:
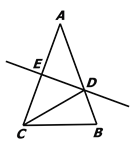
【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.
(1)若∠A = 40°,求∠DCB的度数.
(2)若AE=4,△DCB的周长为13,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
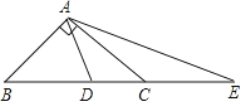
【题目】(1)如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上且CE=CA,试求∠DAE的度数;
(2))如果把第(1)题中“∠BAC=90°”的条件改为“∠BAC>90°”,其余条件不变,那么∠DAE与∠BAC有怎样的数量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表反映的是某地区电的使用量x(千瓦时)与应交电费y(元)之间的关系,下列说法不正确的是( )
用电量x(千瓦时) | 1 | 2 | 3 | 4 | … |
应交电费y(元) | 0.55 | 1.1 | 1.65 | 2.2 | … |
A. x与y都是变量,且x是自变量,y是函数
B. 用电量每增加1千瓦时,电费增加0.55元
C. 若用电量为8千瓦时,则应交电费4.4元
D. y是x的反比例函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com