练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】关于x的一元二次方程x2＋3x-a=0的一个根是2，则a为_____．

    【答案】10.

    【解析】根据一元二次方程的解的定义，将x=2代入关于x的一元二次方程x2+3x-a=0，列出关于a的一元一次方程，通过解方程即可求得a的值.

    解：根据题意知，x=2是关于x的一元二次方程x2+3x-a=0的根，

    ∴22+3×2-a=0，即10-a=0，

    解得a=10.

    故答案为：10.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程x2﹣x+k=0的一个根是2，则k的值是（　　）

    A. ﹣2 B. 2 C. 1 D. ﹣1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数（a＞0）图象的顶点为D，其图象与x轴的交点A、B的横坐标分别为﹣1和3，则下列结论正确的是（ ）

    A. 2a﹣b=0

    B. a+b+c＞0

    C. 3a﹣c=0

    D. 当a=时，△ABD是等腰直角三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将命题“对顶角相等”改写为如果_____________，那么________________的形式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（10分）某商场用2500元购进了A、B两种新型节能台灯共50盏，这两种台灯的进价，标价如下表所示：

    （1）这两种台灯各购进多少盏？

    （2）若A型台灯按标价的九折出售，B型台灯按标价的八折出售，那么这批台灯全部售完后，商场共获利多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=x2+bx+c与x轴交于A，B两点（点A在点B的左侧）与y轴交于点C（0，-3），对称轴是直线x=1，直线BC与抛物线的对称轴交于点D，点E为y轴上一动点，CE的垂直平分线交抛物线于P，Q两点（点P在第三象限）

    （1）求抛物线的函数表达式和直线BC的函数表达式；

    （2）当△CDE是直角三角形，且∠CDE=90° 时，求出点P的坐标；

    （3）当△PBC的面积为时，求点E的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1）所示，E为矩形ABCD的边AD上一点，动点P、Q同时从点B出发，点P沿折线BE-ED-DC运动到点C时停止，点Q沿BC运动到点C时停止，它们运动的速度都是1cm/秒．设P、Q同发t秒时，△BPQ的面积为ycm2．已知y与t的函数关系图象如图（2）（曲线OM为抛物线的一部分），则下列结论：

    ①AD=BE=5；

    ②cos∠ABE=；

    ③当0＜t≤5时，y=t2；

    ④当t=秒时，△ABE∽△QBP；

    其中正确的结论是 （填序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】火车匀速通过隧道时，火车在隧道内的长度（米）与火车行驶时间（秒）之间的关系用图象描述如图所示，有下列结论：

    ①火车的长度为120米；

    ②火车的速度为30米/秒；

    ③火车整体都在隧道内的时间为25秒；

    ④隧道长度为750米．

    其中正确的结论是 ．（把你认为正确结论的序号都填上）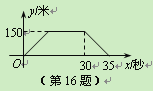

    查看答案和解析>>

    科目：初中数学 来源： 题型：

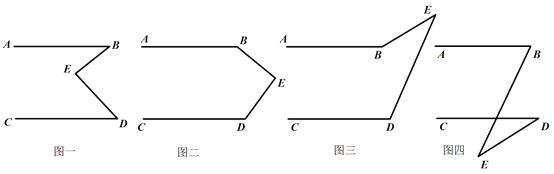
    【题目】有一天李明同学用“几何画板”画图，他先画了两条平行线AB，CD，然后在平行线间画了一点E，连接BE，DE后(如图一)，他用鼠标左键点住点E，拖动后，分别得到如图二，三，四等图形，这时他突然一想，∠B，∠D与∠BED之间的度数有没有某种联系呢？接着李明同学通过利用“几何画板”的“度量角度”和“计算”功能，找到了这三个角之间的关系.

    (1)你能探究出图一到图四各图中的∠B，∠D与∠BED之间的关系吗？

    (2)请从所得的四个关系中，选一个说明它成立的理由.

    查看答案和解析>>

    同步练习册答案