
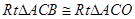 ,点
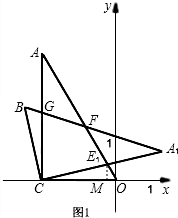
,点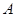 在第二象限内,点
在第二象限内,点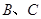 在
在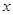 轴的负半轴上,
轴的负半轴上,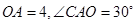 .
.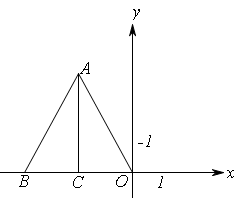
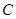 的坐标;
的坐标;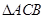 绕点
绕点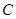 按顺时针方向旋转
按顺时针方向旋转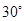 到
到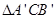 的位置,其中
的位置,其中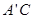 交直线
交直线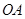 于点
于点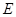 ,
,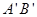 分别交直线
分别交直线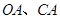 于点
于点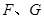 ,则除
,则除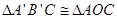 外,还有哪几对全等的三角形,请直接写出答案(不再另外添加辅助线);
外,还有哪几对全等的三角形,请直接写出答案(不再另外添加辅助线);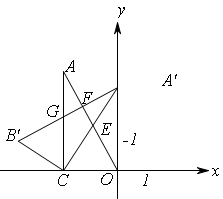
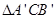 绕点
绕点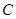 按顺时针方向继续旋转,当
按顺时针方向继续旋转,当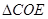 的面积为
的面积为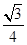 时,求直线
时,求直线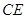 的函数表达式.
的函数表达式.
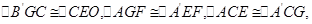
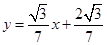 或
或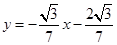
 /4,
/4, /4,
/4, /4,
/4, /4)。
/4)。 /4,
/4, /7,b1=2
/7,b1=2 /7,
/7, /7x+2
/7x+2 /7。
/7。

科目:初中数学 来源:不详 题型:单选题
 或
或 的延长线上,那么∠EMF的度数是
的延长线上,那么∠EMF的度数是
| A.85° | B.90° | C.95° | D.100° |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.5 5米 | B.5 5.5米 | C.5 6米 | D.5 6.5米 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.如果两个三角形全等,则它们必是关于直线成轴对称的图形 |
| B.如果两个三角形关于某直线成轴对称,那么它们是全等三角形 |
| C.等腰三角形的对称轴是底边中线. |
| D.一条线段是关于经过该线段中点的直线成轴对称的图形 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
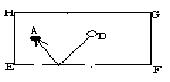
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com