练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

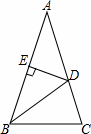
    如图，在△ABC中，AB=AC，∠A=36°，BD为角平分线，DE⊥AB，垂足为E．

    （1）写出图中一对全等三角形和一对相似比不为1的相似三角形；

    （2）选择（1）中一对加以证明．


    解：（1）△ADE≌△BDE，△ABC∽△BCD；

    （2）证明：∵AB=AC，∠A=36°，

    ∴∠ABC=∠C=72°，

    ∵BD为角平分线，

    ∴∠ABD=∠ABC=36°=∠A，

    在△ADE和△BDE中

    ∵，

    ∴△ADE≌△BDE（AAS）；

    证明：∵AB=AC，∠A=36°，

    ∴∠ABC=∠C=72°，

    ∵BD为角平分线，

    ∴∠DBC=∠ABC=36°=∠A，

    ∵∠C=∠C，

    ∴△ABC∽△BCD．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2014-2015学年江苏省滨海县八年级上学期期末考试数学试卷（解析版） 题型：解答题

    （本题满分10分）某剧院举行专场音乐会，成人票每张20元，学生票每张5元，暑假期间，为了丰富广大师生的业余文化生活，剧院制定了两种优惠方案，方案一：购买一张成人票赠送一张学生票；方案二：按总价的90%付款，某校有4名老师与若干名（不少于4人）学生听音乐会．

    （1）设学生人数为x（人），分别求出方案一、方案二的付款总金额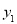、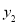（元）与x的函数表达式；

    （2）学生人数在什么范围内，两种方案费用一样？人数在什么范围内，选方案一较划算？人数在什么范围内，选方案二较划算？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某服装店购进单价为15元童装若干件，销售一段时间后发现：当销售价为25元时平均每天能售出8件，而当销售价每降低2元，平均每天能多售出4件．当每件的定价为          元时，该服装店平均每天的销售利润最大．

        

    查看答案和解析>>

    科目：初中数学 来源： 题型：


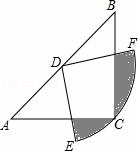
    如图，在△ABC中，CA=CB，∠ACB=90°，以AB的中点D为圆心，作圆心角为90°的扇形DEF，点C恰在EF上，设∠BDF=α（0°＜α＜90°），当α由小到大变化时，图中阴影部分的面积（　　）

    　

    A．

    由小到大

    B．

    由大到小

    　

    C．

    不变

    D．

    先由小到大，后由大到小

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，点A的坐标为（0，6），将△OAB沿x轴向左平移得到△O′A′B′，点A的对应点A′落在直线y=﹣x上，则点B与其对应点B′间的距离为　8　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    定义：数学活动课上，乐老师给出如下定义：有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形．

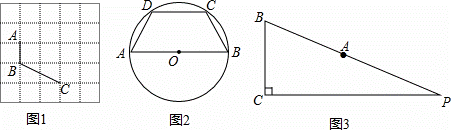
    理解：（1）如图1，已知A、B、C在格点（小正方形的顶点）上，请在方格图中画出以格点为顶点，AB、BC为边的两个对等四边形ABCD；

    （2）如图2，在圆内接四边形ABCD中，AB是⊙O的直径，AC=BD．求证：四边形ABCD是对等四边形；

    （3）如图3，在Rt△PBC中，∠PCB=90°，BC=11，tan∠PBC=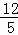，点A在BP边上，且AB=13．用圆规在PC上找到符合条件的点D，使四边形ABCD为对等四边形，并求出CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若代数式+有意义，则实数x的取值范围是（　　）

    　

    A．

    x≠1

    B．

    x≥0

    C．

    x≠0

    D．

    x≥0且x≠1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


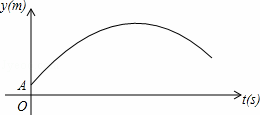
    如图，某足球运动员站在点O处练习射门，将足球从离地面0.5m的A处正对球门踢出（点A在y轴上），足球的飞行高度y（单位：m）与飞行时间t（单位：s）之间满足函数关系y=at2+5t+c，已知足球飞行0.8s时，离地面的高度为3.5m．

    （1）足球飞行的时间是多少时，足球离地面最高？最大高度是多少？

    （2）若足球飞行的水平距离x（单位：m）与飞行时间t（单位：s）之间具有函数关系x=10t，已知球门的高度为2.44m，如果该运动员正对球门射门时，离球门的水平距离为28m，他能否将球直接射入球门？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


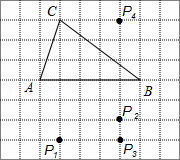
    如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有（　　）

    　

    A．

    1个

    B．

    2个

    C．

    3个

    D．

    4个

     

    查看答案和解析>>

    同步练习册答案