
定义:数学活动课上,乐老师给出如下定义:有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形.
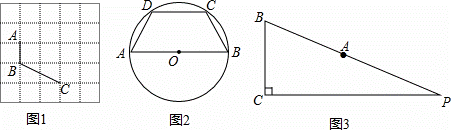
理解:(1)如图1,已知A、B、C在格点(小正方形的顶点)上,请在方格图中画出以格点为顶点,AB、BC为边的两个对等四边形ABCD;
(2)如图2,在圆内接四边形ABCD中,AB是⊙O的直径,AC=BD.求证:四边形ABCD是对等四边形;
(3)如图3,在Rt△PBC中,∠PCB=90°,BC=11,tan∠PBC=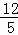 ,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D,使四边形ABCD为对等四边形,并求出CD的长.
,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D,使四边形ABCD为对等四边形,并求出CD的长.
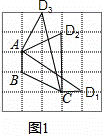
解:(1)如图1所示(画2个即可).
(2)如图2,连接AC,BD,
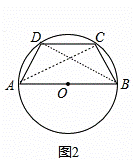
∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
在Rt△ADB和Rt△ACB中,
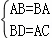
∴Rt△ADB≌Rt△ACB,
∴AD=BC,
又∵AB是⊙O的直径,
∴AB≠CD,
∴四边形ABCD是对等四边形.
(3)如图3,点D的位置如图所示:

①若CD=AB,此时点D在D1的位置,CD1=AB=13;
②若AD=BC=11,此时点D在D2、D3的位置,AD2=AD3=BC=11,
过点A分别作AE⊥BC,AF⊥PC,垂足为E,F,
设BE=x,
∵tan∠PBC=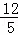 ,
,
∴AE=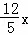 ,
,
在Rt△ABE中,AE2+BE2=AB2,
即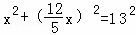 ,
,
解得:x1=5,x2﹣5(舍去),
∴BE=5,AE=12,
∴CE=BC﹣BE=6,
由四边形AECF为矩形,可得AF=CE=6,CF=AE=12,
在Rt△AFD2中,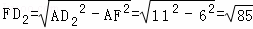 ,
,
∴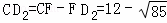 ,
,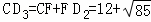 ,
,
综上所述,CD的长度为13、12﹣ 或12+
或12+


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源:2014-2015学年江苏省滨海县八年级上学期期末考试数学试卷(解析版) 题型:解答题
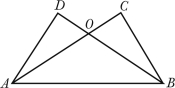
(本题满分8分)如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:△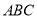 ≌△
≌△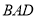 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
某化妆品专卖店,为了吸引顾客,在“母亲节”当天举办了甲、乙两种品牌化妆品有奖酬宾活动,凡购物满88元,均可得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机中一次连续摇出两个球,根据球的颜色决定送礼金券的多少(如下表):
| 甲种品牌 化妆品 | 球 | 两红 | 一红一白 | 两白 |
| 礼金卷(元) | 6 | 12 | 6 |
| 乙种品牌 化妆品 | 球 | 两红 | 一红一白 | 两白 |
| 礼金卷(元) | 12 | 6 | 12 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率;
(2)如果一个顾客当天在本店购物满88元,若只考虑获得最多的礼品卷,请你帮助分析选择购买哪种品牌的化妆品?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
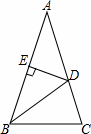
如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.
(1)写出图中一对全等三角形和一对相似比不为1的相似三角形;
(2)选择(1)中一对加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法正确的是( )
|
| A. | “购买1张彩票就中奖”是不可能事件 |
|
| B. | “掷一次骰子,向上一面的点数是6”是随机事件 |
|
| C. | 了解我国青年人喜欢的电视节目应作全面调查 |
|
| D. | 甲、乙两组数据,若S甲2>S乙2,则乙组数据波动大 |
查看答案和解析>>
科目:初中数学 来源: 题型:
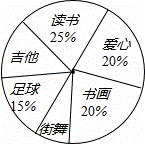
901班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有15人,请解答下列问题:
(1)该班的学生共有 60 名;
(2)若该班参加“吉他社”与“街舞社”的人数相同,请你计算,“吉他社”对应扇形的圆心角的度数;
(3)901班学生甲、乙、丙是“爱心社”的优秀社员,现要从这三名学生中随机选两名学生参加“社区义工”活动,请你用画树状图或列表的方法求出恰好选中甲和乙的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com