
 如图,∠BAC=90°,BF平分∠ABC交AC于F,EF⊥BC于E,AD⊥BC于D,交BF于G.求证:四边形AGEF为菱形.
如图,∠BAC=90°,BF平分∠ABC交AC于F,EF⊥BC于E,AD⊥BC于D,交BF于G.求证:四边形AGEF为菱形. 分析 先证明四边形AGEF是平行四边形,根据AF=EF即可证得.
解答 证明:∵BF平分∠ABC,
∴AF=EF.
∵AD⊥BC,EF⊥BC,
∴∠ADE=∠FEC=90°,
∴AD∥EF,
∴∠AGF=∠BFE.
∵Rt△ABF和Rt△EBF中,
$\left\{\begin{array}{l}{AF=EF}\\{BF=BF}\end{array}\right.$
∴Rt△ABF≌Rt△EBF,
∴∠AFB=∠BFE,
∴∠AGF=∠AFG,
∴AG=AF,
∴AG=EF,
又∵AG∥EF,
∴四边形AGEF是平行四边形.
∵AF=EF,
∴平行四边形AGEF是菱形.
点评 本题考查菱形的判定和性质、全等三角形的判定和性质、平行四边形的判定和性质、直角三角形30度角的性质等知识,寻找全等三角形是解题的关键,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 实数a、b在数轴上的对应点如图所示,请你化简:$\sqrt{a^2}$-$\sqrt{b^2}$+$\sqrt{{{({a-b})}^2}}$.
实数a、b在数轴上的对应点如图所示,请你化简:$\sqrt{a^2}$-$\sqrt{b^2}$+$\sqrt{{{({a-b})}^2}}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
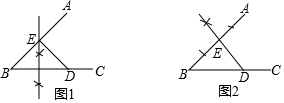
| A. | 甲、乙两名同学的作法均正确 | |
| B. | 甲、乙两名同学的作法均不正确 | |
| C. | 甲同学的作法正确,乙同学的作法不正确 | |
| D. | 甲同学的作法不正确,乙同学的作法正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1-5%)a(1-2x)元 | B. | (1-5%)a(1-x)2元 | C. | (a-5%)(a-2)x元 | D. | a(1-5%-2x)元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
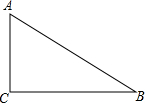 如图,在△ABC中,∠C=90°,∠B=37°,若BC=3.求:AC、AB的长(结果保留小数点后一位).参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.
如图,在△ABC中,∠C=90°,∠B=37°,若BC=3.求:AC、AB的长(结果保留小数点后一位).参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
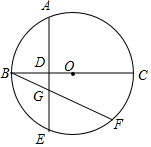 如图,BC是⊙O的直径,弦AE⊥BC,垂足为D点,$\widehat{AB}$=$\frac{1}{2}$$\widehat{BF}$,AE与BF相交于G点.
如图,BC是⊙O的直径,弦AE⊥BC,垂足为D点,$\widehat{AB}$=$\frac{1}{2}$$\widehat{BF}$,AE与BF相交于G点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com