
分析 (1)先根据完全平方公式公式变形,由范围判断x-1、x-2的符号,再根据二次根式和绝对值的性质计算;
(2)先分子$\sqrt{a}$,再根据分式的基本性质分子分母同时约去$\sqrt{a}$-$\sqrt{b}$即可求解.
解答 解:(1)∵x≤1,
∴$\sqrt{{x}^{2}-2x+1}$-$\sqrt{{x}^{2}-4x+4}$
=$\sqrt{(x-1)^{2}}$-$\sqrt{(x-2)^{2}}$
=1-x+x-2
=-1;
(2)$\frac{a-\sqrt{ab}}{\sqrt{a}-\sqrt{b}}$=$\frac{\sqrt{a}(\sqrt{a}-\sqrt{b})}{\sqrt{a}-\sqrt{b}}$=$\sqrt{a}$.
点评 考查了分母有理化,二次根式的性质与化简,(1)的关键是由范围判断x-1、x-2的符号.


科目:初中数学 来源: 题型:解答题
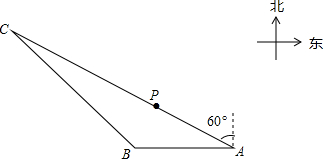 如图.有一艘渔船P在捕鱼作业时出现故障,急需抢修,调度中心通知附近两个小岛A,B上的观测点进行观测,从观测站A测得渔船P在北偏西60°的方向,同时测得搜救船C也在北偏西60°的方向,从观测站B测得渔船P在北偏东32°的方向,测得搜救船C在北偏西45°方向,已知观测站A在观测站B东40里处,问搜救船C与渔船P的距离是多少?(结果保留整数,参考数据:sin32°≈0.53,cos32°≈0.85;tan32°≈0.62,sin58°≈0.85;cos58°≈0.53;tan58°≈1.60;$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73).
如图.有一艘渔船P在捕鱼作业时出现故障,急需抢修,调度中心通知附近两个小岛A,B上的观测点进行观测,从观测站A测得渔船P在北偏西60°的方向,同时测得搜救船C也在北偏西60°的方向,从观测站B测得渔船P在北偏东32°的方向,测得搜救船C在北偏西45°方向,已知观测站A在观测站B东40里处,问搜救船C与渔船P的距离是多少?(结果保留整数,参考数据:sin32°≈0.53,cos32°≈0.85;tan32°≈0.62,sin58°≈0.85;cos58°≈0.53;tan58°≈1.60;$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
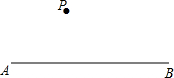 如图,已知点P是直线AB外一点,按下列语句画出图形:
如图,已知点P是直线AB外一点,按下列语句画出图形:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com