13.观察 $\frac{1}{3}$×$\frac{1}{5}$=$\frac{1}{2}(\frac{1}{3}-\frac{1}{5})$,$\frac{1}{5}×\frac{1}{7}$=$\frac{1}{2}$($\frac{1}{5}$-$\frac{1}{7}$),$\frac{1}{7}$×$\frac{1}{9}$=$\frac{1}{2}$($\frac{1}{7}-\frac{1}{9}$)…
计算 $\frac{1}{2}$×$\frac{1}{4}$+$\frac{1}{4}$×$\frac{1}{6}$+$\frac{1}{6}$×$\frac{1}{8}$…+$\frac{1}{2006}$×$\frac{1}{2008}$=$\frac{1003}{4016}$.
分析 原式利用拆项法变形,计算即可得到结果.
解答 解:原式=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{6}$+…+$\frac{1}{2006}$-$\frac{1}{2008}$)=$\frac{1}{2}$×$\frac{1003}{2008}$=$\frac{1003}{4016}$,
故答案为:$\frac{1003}{4016}$
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

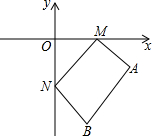 如图,平面直角坐标系xOy中,点A(5,-2)、点B(3,-4),M、N为x轴和y轴上的动点,四边形ABNM的周长最小为10+2$\sqrt{2}$.
如图,平面直角坐标系xOy中,点A(5,-2)、点B(3,-4),M、N为x轴和y轴上的动点,四边形ABNM的周长最小为10+2$\sqrt{2}$.