
��ͼ���ڵ���ֱ�����ǰ�ABC�У�б��BCΪ2����λ���ȣ��ְ�������ǰ���ƽ��ֱ������ϵxOy�л�������ʹB��C����ʼ�շֱ�λ��y�ᡢx����������ϣ�ֱ�Ƕ���A��ԭ��Oλ��BC���࣮
��1��ȡBC�е�D����OD+DA�ij����Ƿ����ı䣬���ᣬ˵�����ɣ������ᣬ���OD+DA���ȣ�
��2������ΪOA�ij����Ƿ�ᷢ���仯�����仯����ôOA��Ƕ��٣�OA�ʱ�ı���OBAC���������ı��Σ���˵�����ɣ�
��3����գ���OA�ʱA�������ǣ� �� ����ֱ��OA�Ľ���ʽ�� ��
(1)2����2��2,������,���ɼ���������3��y=x��
���������������1������ֱ�������ε�б���ϵ����ߵ���б�ߵ�һ�룬���ɵõ�OD=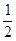 BC=2��
BC=2��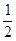 =1���������ǰ���ƶ����ı䣬���OD+DA����ı䣻
=1���������ǰ���ƶ����ı䣬���OD+DA����ı䣻
��2����������֮���߶���̣����ɵõ���O��D��A������һֱ����ʱ��OA���������⣻
��3����O��D��A������һֱ����ʱ��OA����Ҵ�ʱOA�ǵ�һ���Ľ�ƽ���ߣ��ݴ˼�����⣮
���������
�⣺��1��OD=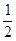 BC=2��
BC=2��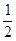 =1����OD+DA=2��
=1����OD+DA=2��
��2����OD=DA=1ʼ�ղ��䣬
�൱O��D��A������һֱ����ʱ��OA�����2��
��ʱ���ı���OBAC�ĶԽ����ཻ�ڵ�D����DO=DB=DA=DC=1��OA=BC=2��
���ı���OBAC�Ǿ��Σ�
�֡�AB=AC��
���ı���OBAC�������Σ�
��3��A�� ��
�� ��
��
ֱ��OA�ǡ�BOC�Ľ�ƽ���ߣ������ʽ�ǣ�y=x��
���㣺1.һ�κ����ۺ��⣻2.����ֱ��������3.���ε����ʼ������ε��ж���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪һ�κ��� ��ͼ���㣨
��ͼ���㣨 ��
�� ������������������
������������������ ��ͼ���ཻ�ڵ㣨4��
��ͼ���ཻ�ڵ㣨4�� ����
����
��1�� ��ֵ��
��ֵ��
��2�� ��
�� ��ֵ��
��ֵ��
��3�����������������ͼ���� ���ཻ�õ��������ε������
���ཻ�õ��������ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪���� ��ͼ����y�ύ�ڵ�A��һ�κ���
��ͼ����y�ύ�ڵ�A��һ�κ��� ��ͼ�� ������B��0����1����������x���Լ�
��ͼ�� ������B��0����1����������x���Լ� ��ͼ��ֱ��ڵ�C��D��
��ͼ��ֱ��ڵ�C��D��
(1)����D�ĺ�����Ϊ1�����ı���AOCD���������ͼ����Ӱ���ֵ��������
(2)�ڵ�(1)С��������£���y�����Ƿ���������ĵ�P��ʹ���Ե�P��B��DΪ������������ǵ��������Σ�������ڣ������P���ꣻ��������ڣ�˵�����ɣ�
(3)��һ�κ��� ��ͼ���뺯��
��ͼ���뺯�� ��ͼ��Ľ���Dʼ���ڵ�һ���ޣ���ϵ��k��ȡֵ��Χ�� ������ֱ��д�������
��ͼ��Ľ���Dʼ���ڵ�һ���ޣ���ϵ��k��ȡֵ��Χ�� ������ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ֱ֪�� ����
����
��1��ֱ���� �ᣬ
�ᣬ ��Ľ������ꣻ
��Ľ������ꣻ
��2�����㣨a,1����ͼ���ϣ���aֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ������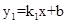 ��ͼ���뺯��
��ͼ���뺯��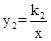 ��
��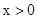 ����ͼ���ڵ�A��2��1����B����y�ύ�ڵ�C��0��3����
����ͼ���ڵ�A��2��1����B����y�ύ�ڵ�C��0��3����
��1������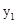 �ı���ʽ�͵�B�����ꣻ
�ı���ʽ�͵�B�����ꣻ
��2���۲�ͼ�Ƚϵ�x��0ʱ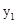 ��
��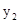 �Ĵ�С��
�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ�����κ��� ��ͼ����x�ύ��������ͬ�ĵ�A����2��0����B��4��0������y�ύ�ڵ�C��0��3��������BC��AC���ö��κ���ͼ��ĶԳ�����x���ཻ�ڵ�D��
��ͼ����x�ύ��������ͬ�ĵ�A����2��0����B��4��0������y�ύ�ڵ�C��0��3��������BC��AC���ö��κ���ͼ��ĶԳ�����x���ཻ�ڵ�D��
��1����������κ����Ľ���ʽ��
��2����D�����꼰ֱ��BC�ĺ�������ʽ��
��3����Q���߶�BC�ϣ�ʹ���Ե�Q��D��BΪ��������������ABC���ƣ������Q�����ꣻ
��4���ڣ�3���������£������ڵ�Q������ѡһ��Q�������BDQ���ԲԲ�ĵ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��ʾһ��������������һ��һ�κ�����ͼ�����ǽ��ڵ�A(4��3)��һ�κ�����ͼ����y�ύ�ڵ�B����OA=OB���������������Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪���������� ��ͼ����һ�κ���
��ͼ����һ�κ��� ��ͼ���ڵ�A��1��4���͵�B
��ͼ���ڵ�A��1��4���͵�B
�� ��
�� ����
����
��1���������������ı���ʽ��
��2���۲�ͼ�� >0ʱ��ֱ��д��
>0ʱ��ֱ��д�� >
>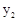 ʱ�Ա���
ʱ�Ա��� ��ȡֵ��Χ��
��ȡֵ��Χ��
��3�������C���A���� ��Գƣ����ABC�������
��Գƣ����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
����ij�̳��мס���������Ʒ������ÿ������15Ԫ���ۼ�20Ԫ������ÿ������35Ԫ���ۼ�45Ԫ��
��1�����̼�ͬʱ�����ס���������Ʒ100���������Ʒ����x���������������Ʒ������Ϊy Ԫ��д��y��x�ĺ�����ϵʽ��
��2�����̼Ҽƻ����Ͷ��3000Ԫ���ڹ�����������Ʒ��100����������Ҫ�������ټ�������Ʒ����������Щ��Ʒ���̼ҿɻ�õ���������Ƕ���Ԫ��
��3������•һ���ڼ䣬�̼ҶԼס���������Ʒ���б��е��Żݻ��С�������̳�һ���Ը���324Ԫ���������Ʒ���̼ҿɻ�õ���С��������������Ƕ��٣�
| ����ǰһ���Թ����ܽ�� | �Żݴ�ʩ |
| ������400Ԫ | �ۼ۴���� |
| ����400Ԫ | �ۼ۴���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com