
如图,已知函数 的图象与y轴交于点A,一次函数
的图象与y轴交于点A,一次函数 的图象 经过点B(0,-1),并且与x轴以及
的图象 经过点B(0,-1),并且与x轴以及 的图象分别交于点C、D.
的图象分别交于点C、D.
(1)若点D的横坐标为1,求四边形AOCD的面积(即图中阴影部分的面积);
(2)在第(1)小题的条件下,在y轴上是否存在这样的点P,使得以点P、B、D为顶点的三角形是等腰三角形.如果存在,求出点P坐标;如果不存在,说明理由.
(3)若一次函数 的图象与函数
的图象与函数 的图象的交点D始终在第一象限,则系数k的取值范围是 .(请直接写出结果)
的图象的交点D始终在第一象限,则系数k的取值范围是 .(请直接写出结果)
(1) ;(2)满足条件的点P有4个:
;(2)满足条件的点P有4个: 、
、 、
、 、
、 ;(3)
;(3) .
.
解析试题分析:本题考查了一次函数综合知识,难度适中,关键是掌握分类讨论思想的运用.(1)如图,连接OD,先求出点D的坐标,再求出BD的解析式,然后根据S四边形AOCD=S△AOD+S△COD即可求解;
(2)求使得以点P、B、D为顶点的三角形是等腰三角形.分三种情况讨论:①当DP=DB时;②当BP=DB时;③当PB=PD时。在三种情况下分别求出点P的坐标.
(3)交点D始终在第一象限,即点D的横坐标x>0.可由交点得到:kx-1=x+1,解得 ,由此可得
,由此可得 ;实际上本题可直接根据图象得出答案.
;实际上本题可直接根据图象得出答案.
试题解析:
解:(1)∵点D的横坐标为1,点D在y=x+1的图象上,
∴D(1,2),
∴直线BD的解析式为y=3x-1,
∴A(0,1),C(13,0),
∴

应分三种情况讨论:如图,
①当DP=DB时,点D位于BP的垂直平分线上,过点D作DE⊥y轴,则BE=PE
∵B(0,-1),D(1,2),
∴BE=BO+OE=1+2=3
∴PE=3
∴PO=5
∴点P的坐标为:
②当BP=DB时,
∴ ,
,
③当PB=PD时,点P位于BD的垂直平分线与y轴的交点上,设P(0,a),
则(a+1)2=1+(2-a)2,
解得:
∴
(3)若一次函数y=kx+b的图象与函数y=x+1的图象的交点D始终在第一象限,则系数k的取值范围是:k>1.
考点:1、一次函数的图象与性质;2、动点问题--构造等腰三角形.


科目:初中数学 来源: 题型:解答题
如图,在直角坐标系xOy中,直线 与双曲线
与双曲线 相交于
相交于 、B
、B 两点,矩形
两点,矩形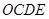 的边
的边 恰好被点
恰好被点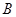 平分,边
平分,边 交双曲线于
交双曲线于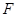 点,四边形
点,四边形 的面积为2.
的面积为2.
(1)求n的值;
(2)求不等式 的解集
的解集
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线 和x轴、y轴的交点分别为B、C,点A的坐标是(
和x轴、y轴的交点分别为B、C,点A的坐标是( ,0),另一条直线经过点A、C.
,0),另一条直线经过点A、C.
(1)求直线AC所对应的函数表达式;
(2)动点M从B出发沿BC运动,运动的速度为每秒1个单位长度.当点M运动到C点时停止运动.设M运动t秒时,△ABM的面积为S.
① 求S与t的函数关系式;
② 当t为何值时, (注:
(注: 表示△ABC的面积),求出对应的t值;
表示△ABC的面积),求出对应的t值;
③当 t=4的时候,在坐标轴上是否存在点P,使得△BMP是以BM为直角边的直角三角形?若存在,请直接写出P点坐标,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距离为s2m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
我市某镇组织20辆汽车装运完A、B、C三种脐橙共100吨到外地销售.按计划,20辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满.根据下表提供的信息,解答以下问题:
(1)设装运A种脐橙的车辆数为 ,装运B种脐橙的车辆数为
,装运B种脐橙的车辆数为 ,求
,求 与
与 之间的函数关系式;
之间的函数关系式;
(2)如果装运每种脐橙的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧.
(1)取BC中点D,问OD+DA的长度是否发生改变,若会,说明理由;若不会,求出OD+DA长度;
(2)你认为OA的长度是否会发生变化?若变化,那么OA最长是多少?OA最长时四边形OBAC是怎样的四边形?并说明理由;
(3)填空:当OA最长时A的坐标是( , ),直线OA的解析式是 .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数 的图象相交于点A(m,1)、B(﹣1,n),与x轴相交于点C(2,0),且AC=
的图象相交于点A(m,1)、B(﹣1,n),与x轴相交于点C(2,0),且AC= OC.
OC.
(1)求该反比例函数和一次函数的解析式;
(2)直接写出不等式ax+b≥ 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com