
小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距离为s2m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
(1)s2=﹣96t+2400;(2)经过20min在返回途中追上爸爸,这时他们距离家还有480m.
解析试题分析:(1)要求s2与t之间的函数关系式,需要找到两个点的坐标, E(0,2400),点F的横坐标是小明的爸爸用的时间25(min),设s2=kt+b,将坐标代入求解;(2)由图知小明从家出发,在返回途中追上爸爸的时间就是两条直线的交点的横坐标,求出直线解析式,就可以求出交点的坐标,从而求出离家的距离.
试题解析:(1)∵小明的爸爸以96m/min速度从邮局同一条道路步行回家,
∴小明的爸爸用的时间为: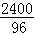 =25(min),
=25(min),
即OF=25,
如图:设s2与t之间的函数关系式为:s2=kt+b,
∵E(0,2400),F(25,0),
∴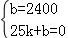 ,解得:
,解得: ,
,
∴s2与t之间的函数关系式为:s2=﹣96t+2400;
(2)如图:小明用了10分钟到邮局,
∴D点的坐标为(22,0),
设直线BD即s1与t之间的函数关系式为:s1=at+c(12≤t≤22),
∴ ,
,
解得: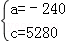 ,
,
∴s1与t之间的函数关系式为:s1=﹣240t+5280(12≤t≤22),
当s1=s2时,小明在返回途中追上爸爸,
即﹣96t+2400=﹣240t+5280,
解得:t=20,
∴s1=s2=480,
∴小明从家出发,经过20min在返回途中追上爸爸,这时他们距离家还有480m.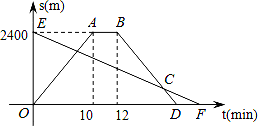
考点:1.一次函数解析式;2.一次函数图象.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:解答题
如图,直线y=- x+6分别与x轴、y轴交于A、B两点;直线y=
x+6分别与x轴、y轴交于A、B两点;直线y= x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿
x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿 轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN,设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN,设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).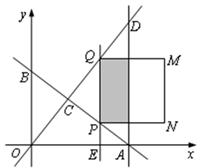
(1)求点C的坐标;
(2)当0<t<5时,求S与t之间的函数关系式,并求S的最大值;
(3)当t>0时,直接写出点(4,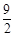 )在正方形PQMN内部时t的取值范围.
)在正方形PQMN内部时t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一次函数 的图象与反比例函数
的图象与反比例函数 的图象交于A(1,4)、B(﹣2,m)两点,
的图象交于A(1,4)、B(﹣2,m)两点,
(1)求一次函数和反比例函数的关系式;
(2)画出草图,并根据草图直接写出不等式 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某公司准备与汽车租赁公司签订租车合同.以每月用车路程x(km)计算,甲汽车租赁公司的月租费 元,乙汽车租赁公司的月租费是
元,乙汽车租赁公司的月租费是 元.如果
元.如果 、
、 与x之间的关系如图所示.
与x之间的关系如图所示.
(1)求 、
、 与x之间的函数关系
与x之间的函数关系
(2)怎样选用汽车租赁比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
小文家与学校相距1000米,某天小文上学时忘了带一本书,走了一段时间才想起,于是返回家拿书,然后加快速度赶到学校,下图是小文与家的距离y(米)关于时间x(分钟)的函数图象。请你根据图象中给出的信息,解答下列问题: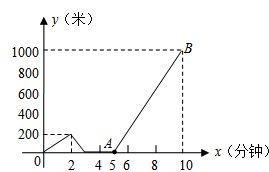
(1)小文走了多远才返回家拿书?
(2)求线段AB所在直线的函数解析式;
(3)当x=8分钟时,求小文与家的距离。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知函数 的图象与y轴交于点A,一次函数
的图象与y轴交于点A,一次函数 的图象 经过点B(0,-1),并且与x轴以及
的图象 经过点B(0,-1),并且与x轴以及 的图象分别交于点C、D.
的图象分别交于点C、D.
(1)若点D的横坐标为1,求四边形AOCD的面积(即图中阴影部分的面积);
(2)在第(1)小题的条件下,在y轴上是否存在这样的点P,使得以点P、B、D为顶点的三角形是等腰三角形.如果存在,求出点P坐标;如果不存在,说明理由.
(3)若一次函数 的图象与函数
的图象与函数 的图象的交点D始终在第一象限,则系数k的取值范围是 .(请直接写出结果)
的图象的交点D始终在第一象限,则系数k的取值范围是 .(请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,矩形OABC的顶点A在y轴正半轴上,点B的横、纵坐标分别是一元二次方程x2+5x﹣24=0的两个实数根,点D是AB的中点.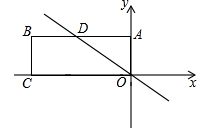
(1)求点B坐标;
(2)求直线OD的函数表达式;
(3)点P是直线OD上的一个动点,当以P、A、D三点为顶点的三角形是等腰三角形时,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,函数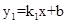 的图象与函数
的图象与函数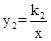 (
(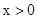 )的图象交于点A(2,1)、B,与y轴交于点C(0,3).
)的图象交于点A(2,1)、B,与y轴交于点C(0,3).
(1)求函数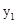 的表达式和点B的坐标;
的表达式和点B的坐标;
(2)观察图象,比较当x>0时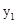 与
与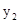 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
△ABC是等边三角形,点A与点D的坐标分别是A(4,0),D(10,0).
(1)如图1,当点C与点O重合时,求直线BD的解析式;
(2)如图2,点C从点O沿y轴向下移动,当以点B为圆心,AB为半径的⊙B与y轴相切(切点为C)时,求点B的坐标;
(3)如图3,点C从点O沿y轴向下移动,当点C的坐标为C 时,求∠ODB的正切值.
时,求∠ODB的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com