解:(1)原方程可变形为

+1+
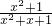
=
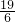
,

+
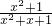
=

.
令y=

,则原方程可变为y+

=

,
解得y
1=

,y
2=

.
当y
1=

时,

=

,解得x=1;
当y
2=

时,

=

,解得x=

.
经检验:x=1或

都是原方程的解.
故原方程的解为x
1=1,x
2=

,x
3=

.
(2)设x
2+2x-8=y,则原方程可化为:
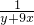
+

+
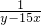
=0,
方程的两边同乘y(y+9x)(y-15x),整理得y
2-4xy-45x
2=0,
解得y=9x或y=-5x.
当y=9x时,x
2+2x-8=9x,x
2-7x-8=0,解得x
1=8,x
2=-1;
当y=-5x时,x
2+2x-8=-5x,x
2+7x-8=0,解得x
3=-8,x
4=1.
经检验:x
1=8,x
2=-1,x
3=-8,x
4=1都是原方程的解.
故原方程的解为x
1=8,x
2=-1,x
3=-8,x
4=1.
(3)[(x+1)(x+4)][(x+2)(x+3)]=120,
(x
2+5x+4)(x
2+5x+6)=120,
设x
2+5x+4=y,则y(y+2)=120,
∴y
2+2y-120=0,
解得y=10或y=-12.
当y=10时,x
2+5x+4=10,x
2+5x-6=0,解得x
1=-6,x
2=1;
当y=-12时,x
2+5x+4=-12,x
2+5x+16=0,△=25-64=-39<0,故此方程无实根.
故原方程的解为x
1=-6,x
2=1.
(4)将原方程变形,得2(x+

)
2-4-3(x+

)=1,
整理,得2(x+

)
2-3(x+

)-5=0.
设x+

=y,则原方程可化为:2y
2-3y-5=0,
解得:y
1=

,y
2=-1.
当y
1=

时,x+

=

,解得:x
1=

,x
2=2;
当y
2=-1时,x+

=-1,即x
2+x+1=0,△=1-4=-3<0,故此方程无实根.
经检验:x
1=

,x
2=2都是原方程的解.
故原方程的解为x
1=

,x
2=2.
分析:(1)由于
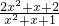
=
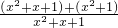
=1+
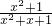
,此时发现两个分式具备倒数关系,
设y=

,则原方程另一个分式为1+

,可用换元法转化为关于y的分式方程.先求y,再求x.结果需检验.
(2)观察发现方程左边三个分式的分母都是关于未知数x的二次三项式,且二次项都是x
2,常数项都是-8,设y=x
2+2x-8,可用换元法转化为关于y的分式方程.先求y,再求x.结果需检验.
(3)先运用乘法交换律与结合律将(x+1)与(x+4)相乘,(x+2)与(x+3)相乘,再设x
2+5x+4=y,
则原方程化为y
2+2y-120=0.用换元法解一元二次方程先求y,再求x.
(4)方程的两个分式具备平方关系,设x+

=y,则原方程化为2y
2-3y-5=0.用换元法解一元二次方程先求y,再求x.注意检验.
点评:本题考查了用换元法解方程.换元法是解方程的常用方法之一,它能够把方程化繁为简,化难为易,对此应注意总结能用换元法解的方程的特点,寻找解题技巧.特别注意解分式方程一定要代入最简公分母验根.

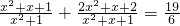 ;
;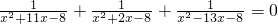 ;
;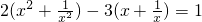 .
. +1+
+1+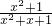 =
=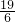 ,
, +
+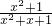 =
= .
. ,则原方程可变为y+
,则原方程可变为y+ =
= ,
, ,y2=
,y2= .
. 时,
时, =
= ,解得x=1;
,解得x=1; 时,
时, =
= ,解得x=
,解得x= .
. 都是原方程的解.
都是原方程的解. ,x3=
,x3= .
.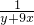 +
+ +
+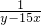 =0,
=0, )2-4-3(x+
)2-4-3(x+ )=1,
)=1, )2-3(x+
)2-3(x+ )-5=0.
)-5=0. =y,则原方程可化为:2y2-3y-5=0,
=y,则原方程可化为:2y2-3y-5=0, ,y2=-1.
,y2=-1. 时,x+
时,x+ =
= ,解得:x1=
,解得:x1= ,x2=2;
,x2=2; =-1,即x2+x+1=0,△=1-4=-3<0,故此方程无实根.
=-1,即x2+x+1=0,△=1-4=-3<0,故此方程无实根. ,x2=2都是原方程的解.
,x2=2都是原方程的解. ,x2=2.
,x2=2.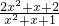 =
=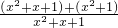 =1+
=1+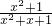 ,此时发现两个分式具备倒数关系,
,此时发现两个分式具备倒数关系, ,则原方程另一个分式为1+
,则原方程另一个分式为1+ ,可用换元法转化为关于y的分式方程.先求y,再求x.结果需检验.
,可用换元法转化为关于y的分式方程.先求y,再求x.结果需检验. =y,则原方程化为2y2-3y-5=0.用换元法解一元二次方程先求y,再求x.注意检验.
=y,则原方程化为2y2-3y-5=0.用换元法解一元二次方程先求y,再求x.注意检验.
