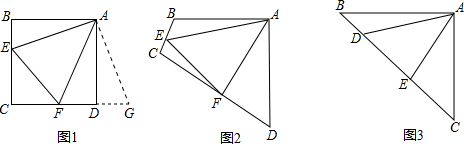
解:

(1)如图①,过P点作PD⊥BO,PH⊥AB,垂足分别为D、H,
∵BC为∠ABO的平分线,
∴PH=PD,
∴S
1:S
2=AB:OB,
又∵OA、OB的长是方程x
2-14x+48=0的两根(OA>OB),
解方程得:x
1=8,x
2=6,
∴OA=8,OB=6,
∴AB=10,
∴S
1:S
2=AB:OB=5:3;
(2)过C点作CK⊥AB,垂足为K,
∴OC=CK,
∴S
△AOB=

OC(OB+AB)=8OC=24,
∴OC=3,
∴C(3,0),
∴y=-2x+6;
(3)①当O、P、E三点共线时,(P在OE与BC交点时)有S
△AOP=S
△AEP,
过E点作EG⊥OA,垂足为G,
∵OE⊥BC,BC平分∠ABO,
∴P是OE的中点,
∴PF是△OEG的中位线,
∵△AGE∽△AOB,
∴
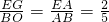
,
∴EG=

,y
P=

,
把y
P=

,代入y=-2x+6中,求得x
P=

,
∴P
1(
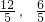
);
②当PA∥OE时,有S
△AOP=S
△AEP,
∴P
2(4,-2).
或用代数方法:设E点坐标为(x,y),根据勾股定理求出
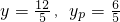
,
再将
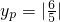
代入y=-2x+6,同样求出P
1(
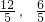
)、P
2(4,-2).
分析:(1)如图①,过P点作PD⊥BO,PH⊥AB,垂足分别为D、H,由BC为∠ABO的平分线,可得PH=PD,则可得S
1:S
2=AB:OB,又∵OA、OB的长是方程x
2-14x+48=0的两根(OA>OB),解方程即可求得OA,OB的长,则可得S
1:S
2的值;
(2)过C点作CK⊥AB,垂足为K,可得OC=CK,由S
△AOB=

OC(OB+AB)=8OC=24,可求得点C的坐标,即即可得直线BC的解析式;
(3)分别从①当O、P、E三点共线时,(P在OE与BC交点时)有S
△AOP=S
△AEP,②当PA∥OE时,有S
△AOP=S
△AEP去分析,利用三角形的面积求解方法,即可求得P点坐标.
点评:此题考查了相似三角形的判定与性质,一次函数的知识,三角形面积的求解方法等知识.此题综合性很强,解题的关键是方程思想与数形结合思想的应用.

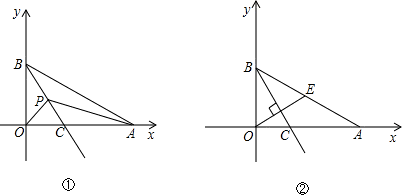

 OC(OB+AB)=8OC=24,
OC(OB+AB)=8OC=24,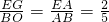 ,
, ,yP=
,yP= ,
, ,代入y=-2x+6中,求得xP=
,代入y=-2x+6中,求得xP= ,
,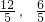 );
);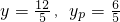 ,
,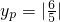 代入y=-2x+6,同样求出P1(
代入y=-2x+6,同样求出P1(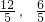 )、P2(4,-2).
)、P2(4,-2). OC(OB+AB)=8OC=24,可求得点C的坐标,即即可得直线BC的解析式;
OC(OB+AB)=8OC=24,可求得点C的坐标,即即可得直线BC的解析式;