
【题目】如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.

(1)若∠A=60°,求BC的长;
(2)若sinA=![]() ,求AD的长.
,求AD的长.
(注意:本题中的计算过程和结果均保留根号)
【答案】(1)6![]() ﹣8;(2)
﹣8;(2)![]() .
.
【解析】
试题分析:(1)根据锐角三角函数求得BE和CE的长,根据BC=BE﹣CE即可求得BC的长;(2)根据题意求得AE和DE的长,由AD=AE﹣DE即可求得AD的长.
试题解析:(1)∵∠A=60°,∠ABE=90°,AB=6,tanA=![]() ,
,
∴∠E=30°,BE=tan60°6=6![]() ,
,
又∵∠CDE=90°,CD=4,sinE=![]() ,∠E=30°,
,∠E=30°,
∴CE=![]() =8,
=8,
∴BC=BE﹣CE=6![]() ﹣8;
﹣8;
(2))∵∠ABE=90°,AB=6,sinA=![]() =
=![]() ,
,
∴设BE=4x,则AE=5x,得AB=3x,
∴3x=6,得x=2,
∴BE=8,AE=10,
∴tanE=![]() =
=![]() =
=![]() =
=![]() ,
,
解得,DE=![]() ,
,
∴AD=AE﹣DE=10﹣![]() =
=![]() ,
,
即AD的长是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BCAD=![]() AE2;④S△ABC=4S△ADF.其中正确的有( )
AE2;④S△ABC=4S△ADF.其中正确的有( )
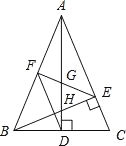
A.1个 B.2 个 C.3 个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
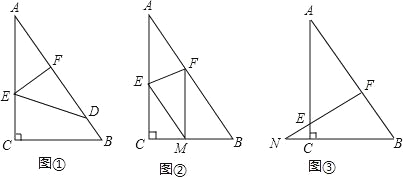
【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上点,连接EF.
(1)图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF,求AE的长;
(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图③,若FE的延长线与BC的延长线交于点N,CN=1,CE=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,若点A (a,﹣b)在第一象限内,则点B (a,b﹣3)所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在¨ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF,BF

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件可以判定△ABC是等腰三角形的是( )
A. 三条边长分别是5, 11,5B. 三条边长分别是 6,6,12
C. 三条边长分别是6,13,6D. 三条边长分别为5,5,4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com