
ΓΨΧβΡΩΓΩΈΣΝΥΙΡάχ –ΟώΫΎ‘Φ”ΟΥ°Θ§Ρ≥ –Ψ”Οώ…ζΜν”ΟΥ°Α¥ΫΉΧί ΫΥ°ΦέΦΤΖ―Θ§±μ «ΗΟ –Ψ”ΟώΓΑ“ΜΜß“Μ±μΓ±…ζΜν”ΟΥ°ΫΉΧί ΫΦΤΖ―ΦέΗώ±μΒΡ“Μ≤ΩΖ÷–≈œΔΘΚΘ®Υ°ΦέΦΤΖ―=Ή‘ά¥Υ°œζ έΖ―”Ο+ΈέΥ°¥ΠάμΖ―”ΟΘ©
Ή‘ά¥Υ°œζ έΦέΗώ | ΈέΥ°¥ΠάμΦέΗώ | |
ΟΩΜßΟΩ‘¬”ΟΥ°ΝΩ | ΒΞΦέΘΚ‘Σ/Ε÷ | ΒΞΦέΘΚ‘Σ/Ε÷ |
17Ε÷ΦΑ“‘œ¬ | a | 0.80 |
≥§Ιΐ17Ε÷≤Μ≥§Ιΐ30Ε÷ΒΡ≤ΩΖ÷ | b | 0.80 |
≥§Ιΐ30Ε÷ΒΡ≤ΩΖ÷ | 6.00 | 0.80 |
“―÷Σ–ΓΆθΦ“2012Ρξ4‘¬Ζί”ΟΥ°20Ε÷Θ§ΫΜΥ°Ζ―66‘ΣΘΜ5‘¬Ζί”ΟΥ°25Ε÷Θ§ΫΜΥ°Ζ―91‘ΣΘ°
Θ®1Θ©«σaΘ§bΒΡ÷ΒΘ°
Θ®2Θ©–ΓΆθΦ“6‘¬ΖίΫΜΥ°Ζ―184‘ΣΘ§‘ρ–ΓΆθΦ“6‘¬Ζί”ΟΥ°Εύ…ΌΕ÷ΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©aΒΡ÷Β «2.2Θ§bΒΡ÷Β «4.4ΘΜΘ®2Θ©–ΓΆθΦ“6‘¬Ζί”ΟΥ°ΝΩ40Ε÷Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΧβ“βΚΆ±μΗώΩ…“‘Ν–≥ωœύ”ΠΒΡΕΰ‘Σ“Μ¥ΈΖΫ≥ΧΉιΘ§¥”ΕχΩ…“‘«σ≥ωaΓΔbΒΡ÷ΒΘΜ
Θ®2Θ©ΗυΨίΧβ“βΩ…“‘Ν–≥ωœύ”ΠΒΡΖΫ≥ΧΘ§¥”ΕχΩ…“‘«σΒΟ–ΓΆθΦ“±Ψ‘¬”ΟΥ°ΝΩΈΣΕύ…ΌΕ÷Θ°
Θ®1Θ©ΗυΨίΧβ“βΩ…ΒΟΘ§
![]() Θ§
Θ§
ΫβΒΟΘ§![]() Θ§
Θ§
Φ¥aΒΡ÷Β «2.2Θ§bΒΡ÷Β «4.4ΘΜ
Θ®2Θ©…η–ΓΆθΦ“6‘¬Ζί”ΟΥ°xΕ÷Θ§
ΗυΨίΧβ“β÷ΣΘ§30Ε÷ΒΡΥ°Ζ―ΈΣΘΚ17ΓΝ2.2+13ΓΝ4.2+30ΓΝ0.8=116Θ§
ΓΏ184ΘΨ116Θ§
Γύ–ΓΆθΦ“6‘¬ΖίΦΤΜ°”ΟΥ°≥§ΙΐΝΥ30Ε÷
Γύ6.0Θ®x©¹30Θ©+116+0.80ΓΝΘ®x©¹30Θ©=184Θ§
ΫβΒΟΘ§x=40
Φ¥–ΓΆθΦ“6‘¬Ζί”ΟΥ°ΝΩ40Ε÷Θ°


 »ΪΡή≤βΩΊΤΎΡ©–ΓΉ¥‘ΣœΒΝ–¥πΑΗ
»ΪΡή≤βΩΊΤΎΡ©–ΓΉ¥‘ΣœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΕΰ¥ΈΚ· ΐy= ![]() x2+bx+cΒΡΆΦœσΨ≠ΙΐΒψAΘ®©¹3Θ§6Θ©Θ§≤Δ”κx÷αΫΜ”ΎΒψBΘ®©¹1Θ§0Θ©ΚΆΒψCΘ§”κy÷αΫΜ”ΎΒψEΘ§ΕΞΒψΈΣPΘ§Ε‘≥Τ÷α”κx÷αΫΜ”ΎΒψD
x2+bx+cΒΡΆΦœσΨ≠ΙΐΒψAΘ®©¹3Θ§6Θ©Θ§≤Δ”κx÷αΫΜ”ΎΒψBΘ®©¹1Θ§0Θ©ΚΆΒψCΘ§”κy÷αΫΜ”ΎΒψEΘ§ΕΞΒψΈΣPΘ§Ε‘≥Τ÷α”κx÷αΫΜ”ΎΒψD
Θ®1Θ©«σ’βΗωΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΘΜ
Θ®2Θ©Ν§Ϋ”CPΘ§ΓςDCP « ≤Ο¥ΧΊ β–ΈΉ¥ΒΡ»ΐΫ«–ΈΘΩ≤ΔΦ”“‘ΥΒΟςΘΜ
Θ®3Θ©ΒψQ «ΒΎ“ΜœσœόΒΡ≈ΉΈοœΏ…œ“ΜΒψΘ§«“¬ζΉψΓœQEO=ΓœBEOΘ§«σ≥ωΒψQΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
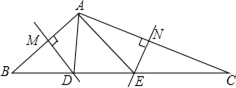
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§±ΏABΓΔACΒΡ¥Ι÷±ΤΫΖ÷œΏΖ÷±πΫΜBC”ΎDΓΔEΘ°
Θ®1Θ©»τBC=5Θ§«σΓςADEΒΡ÷ή≥ΛΘ°
Θ®2Θ©»τΓœBAC=120ΓψΘ§«σΓœDAEΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§Εΰ¥ΈΚ· ΐy=ax2+bx+cΒΡΆΦœσ÷–Θ§ΆθΗ’Ά§―ßΙέ≤λΒΟ≥ωΝΥœ¬ΟφΥΡΧθ–≈œΔΘΚΘ®1Θ©b2©¹4acΘΨ0ΘΜΘ®2Θ©cΘΨ1ΘΜΘ®3Θ©2a©¹bΘΦ0ΘΜΘ®4Θ©a+b+cΘΦ0Θ§Τδ÷–¥μΈσΒΡ”–Θ® Θ©
A.1Ηω
B.2Ηω
C.3Ηω
D.4Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§»Έ“βΥΡ±Ώ–ΈABCD÷–Θ§EΘ§FΘ§GΘ§HΖ÷±π «ABΘ§BCΘ§CDΘ§DA…œΒΡΒψΘ§Ε‘”ΎΥΡ±Ώ–ΈEFGHΒΡ–ΈΉ¥Θ§Ρ≥Αύ―ß…ζ‘Ύ“Μ¥Έ ΐ―ßΜνΕ·ΩΈ÷–Θ§Ά®ΙΐΕ· ÷ ΒΦυΘ§ΧΫΥς≥ω»γœ¬Ϋα¬έΘ§Τδ÷–¥μΈσΒΡ «Θ® Θ©
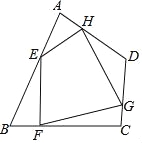
AΘ°Β±EΘ§FΘ§GΘ§H «Ης±Ώ÷–ΒψΘ§«“AC=BD ±Θ§ΥΡ±Ώ–ΈEFGHΈΣΝβ–Έ
BΘ°Β±EΘ§FΘ§GΘ§H «Ης±Ώ÷–ΒψΘ§«“ACΓΆBD ±Θ§ΥΡ±Ώ–ΈEFGHΈΣΨΊ–Έ
CΘ°Β±EΘ§FΘ§GΘ§H≤Μ «Ης±Ώ÷–Βψ ±Θ§ΥΡ±Ώ–ΈEFGHΩ…“‘ΈΣΤΫ––ΥΡ±Ώ–Έ
DΘ°Β±EΘ§FΘ§GΘ§H≤Μ «Ης±Ώ÷–Βψ ±Θ§ΥΡ±Ώ–ΈEFGH≤ΜΩ…ΡήΈΣΝβ–Έ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τΤΫ––ΥΡ±Ώ–ΈABCDΒΡ“ΜΗωΫ«ΒΡΤΫΖ÷œΏΑ―“ΜΧθ±ΏΖ÷≥…≥Λ «4cmΚΆ5cmΒΡΝΫΧθœΏΕΈΘ§‘ρΤΫ––ΥΡ±Ώ–ΈABCDΒΡ÷ή≥Λ «__________cmΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ![]() «Ήν–ΓΒΡΝΫΈΜ’ΐ’ϊ ΐΘ§«“
«Ήν–ΓΒΡΝΫΈΜ’ΐ’ϊ ΐΘ§«“![]() ΓΔ
ΓΔ![]() ¬ζΉψ
¬ζΉψ![]() «κΜΊ¥πΈ ΧβΘΚ
«κΜΊ¥πΈ ΧβΘΚ
Θ®1Θ©«κ÷±Ϋ”–¥≥ω![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΒΡ÷ΒΘΚ
ΒΡ÷ΒΘΚ![]()
![]()
![]()
Θ®2Θ©‘Ύ ΐ÷α…œ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΥυΕ‘”ΠΒΡΒψΖ÷±πΈΣ
ΥυΕ‘”ΠΒΡΒψΖ÷±πΈΣ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]()
ΔΌΦ«![]() ΓΔ
ΓΔ![]() ΝΫΒψΦδΒΡΨύάκΈΣ
ΝΫΒψΦδΒΡΨύάκΈΣ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§![]() ΘΜ
ΘΜ
ΔΎΒψ![]() ΈΣΗΟ ΐ÷αΒΡΕ·ΒψΘ§ΤδΕ‘”ΠΒΡ ΐΈΣxΘ§Βψ
ΈΣΗΟ ΐ÷αΒΡΕ·ΒψΘ§ΤδΕ‘”ΠΒΡ ΐΈΣxΘ§Βψ![]() ‘ΎΒψ
‘ΎΒψ![]() ”κΒψ
”κΒψ![]() ÷°Φδ‘ΥΕ· ±Θ®ΑϋΚ§ΕΥΒψΘ©Θ§‘ρ
÷°Φδ‘ΥΕ· ±Θ®ΑϋΚ§ΕΥΒψΘ©Θ§‘ρ![]() Θ§
Θ§![]() .
.
Θ®3Θ©‘ΎΘ®1Θ©Θ®2Θ©ΧθΦΰœ¬Θ§»τΒψ![]() ¥”
¥”![]() ≥ωΖΔΘ§“‘ΟΩΟκ
≥ωΖΔΘ§“‘ΟΩΟκ![]() ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρΒψ
ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρΒψ![]() “ΤΕ·Θ§Β±Βψ
“ΤΕ·Θ§Β±Βψ![]() ‘ΥΕ·ΒΫ
‘ΥΕ·ΒΫ![]() Βψ ±Θ§Βψ
Βψ ±Θ§Βψ![]() ¥”
¥”![]() ≥ωΖΔΘ§“‘ΟΩΟκ
≥ωΖΔΘ§“‘ΟΩΟκ![]() ΗωΒΞΈΜ≥ΛΕ»œρ
ΗωΒΞΈΜ≥ΛΕ»œρ![]() Βψ‘ΥΕ·Θ§ΒψMΓΔ
Βψ‘ΥΕ·Θ§ΒψMΓΔ![]() ΒΫ¥ο
ΒΫ¥ο![]() ΒψΚσΘ§‘ΌΝΔΦ¥“‘Ή‘…μΆ§―υΒΡΥΌΕ»ΖΒΜΊΒψ
ΒψΚσΘ§‘ΌΝΔΦ¥“‘Ή‘…μΆ§―υΒΡΥΌΕ»ΖΒΜΊΒψ![]() . …ηΒψ
. …ηΒψ![]() “ΤΕ· ±ΦδΈΣ
“ΤΕ· ±ΦδΈΣ![]() ΟκΘ§Β±Βψ
ΟκΘ§Β±Βψ![]() ΩΣ Φ‘ΥΕ·ΚσΘ§«κ”ΟΚ§
ΩΣ Φ‘ΥΕ·ΚσΘ§«κ”ΟΚ§![]() ΒΡ¥ζ ΐ Ϋ±μ Ψ
ΒΡ¥ζ ΐ Ϋ±μ Ψ![]() ΓΔ
ΓΔ![]() ΝΫΒψΦδΒΡΨύάκ.
ΝΫΒψΦδΒΡΨύάκ.
![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ≥Χ¥σΈΜΥυ÷χΓΕΥψΖ®Ά≥ΉΎΓΖ «“Μ≤Ω÷–Ιζ¥ΪΆ≥ ΐ―ß÷Ί“ΣΒΡ÷χΉςΘ°‘ΎΓΕΥψΖ®Ά≥ΉΎΓΖ÷–Φ«‘ΊΘΚΓΑΤΫΒΊ«ο«ßΈ¥ΤπΘ§ΧΛΑεάκΒΊ“Μ≥ΏΘ°ΥΆ––Εΰ≤Ϋ”κ»ΥΤκΘ§Έε≥Ώ»ΥΗΏ‘χΦ«Θ° Υ≈°Φ―»Υ’υθμΘ§÷’≥·–Π”οΜΕφ“Θ°ΝΦΙΛΗΏ ΩΥΊΚΟΤφΘ§Υψ≥ωΥς≥Λ”–ΦΗΘΩΓ±ΓΨΉΔ ΆΓΩ1≤Ϋ=5≥ΏΘ°
“κΈΡΘΚΓΑΒ±«ο«ßΨ≤÷Ι ±Θ§«ο«ß…œΒΡΧΛΑεάκΒΊ”–1≥ΏΗΏΘ§»γΫΪ«ο«ßΒΡΧΛΑεΆυ«ΑΆΤΕ·ΝΫ≤ΫΘ®10≥ΏΘ© ±Θ§ΧΛΑεΨΆΚΆ»Υ“Μ―υΗΏΘ§“―÷Σ’βΗω»Υ…μΗΏ «5≥ΏΘ°ΟάάωΒΡΙΟΡοΚΆ≤≈Ή”Ο«Θ§ΟΩΧλΕΦά¥’υΒ¥«ο«ßΘ§ΜΕ…υ–Π”ο÷’»’≤ΜΕœΘ°ΚΟΤφΒΡΡήΙΛ«…Ϋ≥Θ§ΡήΥψ≥ω’β«ο«ßΒΡ…ΰΥς≥Λ «Εύ…Ό¬πΘΩΓ±
»γΆΦΘ§ΦΌ…η«ο«ßΒΡ…ΰΥς≥Λ Φ÷’±Θ≥÷÷±œΏΉ¥Χ§Θ§OA ««ο«ßΒΡΨ≤÷ΙΉ¥Χ§Θ§A «ΧΛΑεΘ§CD «ΒΊΟφΘ§ΒψB «ΆΤΕ·ΝΫ≤ΫΚσΧΛΑεΒΡΈΜ÷ΟΘ§ΜΓAB «ΧΛΑε“ΤΕ·ΒΡΙλΦΘΘ°“―÷ΣAC=1≥ΏΘ§CD=EB=10≥ΏΘ§»ΥΒΡ…μΗΏBD=5≥ΏΘ°…η…ΰΥς≥ΛOA=OB=x≥ΏΘ§‘ρΩ…Ν–ΖΫ≥ΧΈΣ Θ° 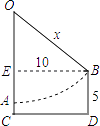
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ≈ΉΈοœΏy=x2+Θ®b©¹1Θ©x©¹5Θ°
Θ®1Θ©–¥≥ω≈ΉΈοœΏΒΡΩΣΩΎΖΫœρΚΆΥϋ”κy÷αΫΜΒψΒΡΉχ±ξΘΜ
Θ®2Θ©»τ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΈΣ÷±œΏx=1Θ§«σbΒΡ÷ΒΘ§≤ΔΜ≠≥ω≈ΉΈοœΏΒΡ≤ίΆΦΘ®≤Μ±ΊΝ–±μΘ©ΘΜ
Θ®3Θ©»γΆΦΘ§»τbΘΨ3Θ§Ιΐ≈ΉΈοœΏ…œ“ΜΒψPΘ®©¹1Θ§cΘ©Ής÷±œΏPAΓΆy÷αΘ§¥ΙΉψΈΣAΘ§ΫΜ≈ΉΈοœΏ”ΎΝμ“ΜΒψBΘ§«“BP=2PAΘ§«σ’βΧθ≈ΉΈοœΏΥυΕ‘”ΠΒΡΕΰ¥ΈΚ· ΐΫβΈω ΫΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com