
 如图:人民海关缉私巡逻艇在东海执行巡逻任务时,发现在其所在位置O点的北偏西30°方向40海里的A点有一走私船正向正东方向航行,1小时后,测得走私船在O点的北偏东30°方向的B点.
如图:人民海关缉私巡逻艇在东海执行巡逻任务时,发现在其所在位置O点的北偏西30°方向40海里的A点有一走私船正向正东方向航行,1小时后,测得走私船在O点的北偏东30°方向的B点.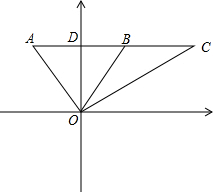
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |


科目:初中数学 来源:数学教研室 题型:044
如图所示,人民海关缉私巡逻艇在东海海域执行巡逻任务时,发现在其所处位置O点的正北方向10海里的A点有一涉嫌走私船只,正以 海里/时的速度向正东方向航行,为了迅速实施检查,巡逻艇调整好航向,以20海里/时的速度追赶,在涉嫌船只不改变航向和航速的前提下,问:
海里/时的速度向正东方向航行,为了迅速实施检查,巡逻艇调整好航向,以20海里/时的速度追赶,在涉嫌船只不改变航向和航速的前提下,问:
(1)需要几小时才能追上?(点B为追上时的位置)
(2)确定巡逻艇的追赶方向.

查看答案和解析>>
科目:初中数学 来源:黄冈难点课课练 八年级数学上册 题型:044
如图,人民海关缉私巡逻艇在东海海域执行巡逻任务时,发现其所处位置O点的正北方向10海里处的A点有一涉嫌走私船只正以24海里/时的速度向正东方向航行,为迅速实施检查,巡逻艇调整好航向,以26海里/时的速度追赶,在涉嫌船只不改变航向和航速的前提下,要几小时才能追上?
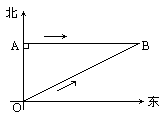
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
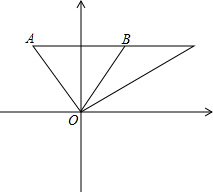 如图:人民海关缉私巡逻艇在东海执行巡逻任务时,发现在其所在位置O点的北偏西30°方向40海里的A点有一走私船正向正东方向航行,1小时后,测得走私船在O点的北偏东30°方向的B点.
如图:人民海关缉私巡逻艇在东海执行巡逻任务时,发现在其所在位置O点的北偏西30°方向40海里的A点有一走私船正向正东方向航行,1小时后,测得走私船在O点的北偏东30°方向的B点.查看答案和解析>>
科目:初中数学 来源:2012年浙江省台州市三门中学中考数学模拟试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com