
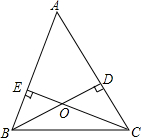
 如图,在△ABC中,BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE相交于点O.
如图,在△ABC中,BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE相交于点O.分析 (1)根据四边形的内角和是360°,用360°减去∠A、∠AEC、∠ADB的度数和,求出∠DOE的度数,然后根据对顶角相等,求出∠BOC的度数是多少即可;
(2)因为∠DOE+∠A=180°,所以∠DOE与∠A互补,因此∠BOC与∠A互补,据此解答即可.
解答 解:(1)∵∠A=50°,
∴∠DOE=360°-(∠A+∠AEC+∠ADB)
=360°-(50°+90°+90°)
=360°-230°
=130°
∵∠BOC和∠DOE是对顶角,
∴∠BOC=130°.
(2)∵∠DOE+∠A=130°+50°=180°,
∴∠DOE与∠A互补,
∴∠BOC与∠A互补.
点评 (1)此题主要考查了四边形的内角和问题,要熟练掌握,解答此题的关键是要明确:四边形的内角和是360°.
(2)此题还考查了对顶角、互补角的含义以及应用,解答此题的关键是要明确:同一平面内两角相加为180°,这两个角两个角叫互补角互补角.


科目:初中数学 来源: 题型:解答题
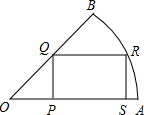 如图,扇形中∠AOB=45°,半径OB=2,矩形PQRS的顶点P、S在半径OA上,Q在半径OB上,R在弧AB上,连接OR.
如图,扇形中∠AOB=45°,半径OB=2,矩形PQRS的顶点P、S在半径OA上,Q在半径OB上,R在弧AB上,连接OR.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当m=0时,二次函数图象的顶点坐标为(0,0) | |
| B. | 当m<0时,二次函数图象的对称轴在y轴右侧 | |
| C. | 设二次函数的图象与y轴交点为A,过A作x轴的平行线,交图象于另一点B,抛物线的顶点为C,则△ABC的面积为m3 | |
| D. | 该函数图象沿y轴向下平移6个单位后,图象与x轴两交点之间的距离为2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com