练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．已知在△ABC中，∠A=2∠C，∠B=3∠C，求各内角的度数，并判断△ABC的形状．

    分析 首先根据三角形的内角和定理，可得2∠C+3∠C+∠C=180°，据此求出∠C的度数是多少，进而求出∠A、∠B的度数是多少；然后根据三角形的三个内角的特征，判断出△ABC的形状即可．

    解答 解：∵∠A=2∠C，∠B=3∠C，
    ∴2∠C+3∠C+∠C=180°，
    ∴6∠C=180°，
    解得∠C=30°；
    ∴∠A=2∠C=2×30°=60°，
    ∠B=3∠C=3×30°=90°，
    ∴△ABC是直角三角形．

    点评 （1）此题主要考查了三角形的内角和定理，要熟练掌握，解答此题的关键是要明确：三角形的内角和是180°，并能求出每个内角的度数是多少．
    （2）此题还考查了直角三角形的三个内角的特征，要熟练掌握．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    11．若将分式$\frac{a+b}{2ab}$中的字母a，b的值分别扩大到原来的2倍，则分式的值（　　）
    A．扩大到原来的2倍B．缩小到原来的$\frac{1}{2}$C．缩小到原来的$\frac{1}{4}$D．不变

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．解不等式：$\frac{1}{3}$（x-3）+2≤-$\frac{5+x}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．整数k为何值时，二元一次方程组$\left\{\begin{array}{l}{2x-y=3k+1}\\{3x+y=2k-5}\end{array}\right.$的解均为非正数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知$\frac{1}{x}+\frac{1}{y}=\frac{1}{4}$，求$\frac{3x-4xy+3y}{-x+5xy-y}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

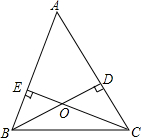    6．如图，在△ABC中，BD⊥AC，CE⊥AB，垂足分别为D、E，BD、CE相交于点O．
    （1）已知∠A=50°，求∠BOC的度数；
    （2）探究∠BOC与∠A的关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

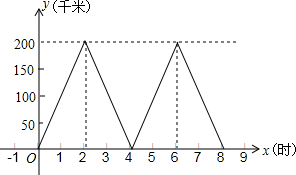    13．某物流公司的快递车和货车每天往返于A、B两地，快递车比物流车多往返一趟．如图表示快递车距离A地的路程与所用时间的函数图象．已知货车比快递车早1小时出发，到达B地后用2小时装卸货物，然后按原路、原速返回，结果比快递车最后一次返回A地晚1小时．
    （1）请在图中画出货车距离A地的路与所用时间函数图象；
    （2）两车在途中相遇4次．
    （3）若快递车的速度是每小时100千米，货车的速度是每小时50千米，问：两车第一次相遇时，快递车从A地出发了几小时？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知圆O，
    （1）求作圆O的内接正六边形ABCDEF；（要求尺规作图，保留作图痕迹）
    （2）若圆O的半径为2，计算弦AB与弧$\widehat{AB}$所形成的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．（1）计算：（6.28-2π）0+（-$\frac{1}{6}$）-2-2cos60°；
    （2）解方程：$\frac{3}{x-7}$=$\frac{2}{x-8}$．

    查看答案和解析>>

    同步练习册答案