
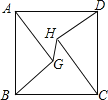
【题目】如图正方形ABCD边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 10-5
D. 10-5![]()
科目:初中数学 来源: 题型:
【题目】为估计某水库鲢鱼的数量,养鱼户李老板先捞上150条鲢鱼并在鲢鱼身上做红色的记号,然后立即将这150条鲢鱼放回水库中,一周后,李老板又捞取200条鲢鱼,发现带红色记号的鱼有三条,据此可估计出该水库中鲢鱼约有________条.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中是真命题的是( )
A. 有一个角相等的直角三角形都相似
B. 有一个角相等的等腰三角形都相似
C. 有一个角是120°的等腰三角形都相似
D. 两边成比例且有一角相等的三角形都相似
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某移动公司开设了两种通信业务:“全球通”要缴月租费50元。另外每分钟通话费0.4元;“神州行”不缴月租费,但每分钟通话费0.6元.若一个月通话![]() ,两种收费方式的费用分别为
,两种收费方式的费用分别为![]() 和
和![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式?
的函数解析式?
(2)一个月内通话多少分钟,两种收费方式的费用是相同的?
(3)=若![]() ,选择哪种收费方式更合适?
,选择哪种收费方式更合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲厂有某种原料180吨,运出2x吨,乙厂有同样的原料120吨,运进x吨,现在甲厂原料比乙厂原料多30吨,根据题意列方程,则下列所列方程正确的是( )
A.(180﹣2x)﹣(120+x)=30
B.(180+2x)﹣(120﹣x)=30
C.(180﹣2x)﹣(120﹣x)=30
D.(180+2x)﹣(120+x)=30
查看答案和解析>>
科目:初中数学 来源: 题型:
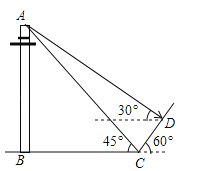
【题目】黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.
(结果精确到1m,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们对多项式x2+x-6进行因式分解时,可以用特定系数法求解.例如,我们可以先设x2+x-6=(x+a)(x+b),显然这是一个恒等式.根据多项式乘法将等式右边展开有:x2+x-6=(x+a)(x+b)=x2+(a+b)x+ab
所以,根据等式两边对应项的系数相等,可得:a+b=1,ab=-6,解得a=3,b=-2或者a=-2,b=3.所以x2+x-6=(x+3)(x-2).当然这也说明多项式x2+x-6含有因式:x+3和x-2.
像上面这种通过利用恒等式的性质来求未知数的方法叫特定系数法.利用上述材料及示例解决以下问题.
(1)已知关于x的多项式x2+mx-15有一个因式为x-1,求m的值;
(2)已知关于x的多项式2x3+5x2-x+b有一个因式为x+2,求b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com