
在平面直角坐标系中,抛物线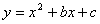 与
与 轴交于A、B两点(点A在点B的左侧),与
轴交于A、B两点(点A在点B的左侧),与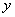 轴交于点C,点B的坐标为(3,0),将直线
轴交于点C,点B的坐标为(3,0),将直线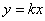 沿
沿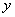 轴向上平移3个单位长度后恰好经过B、C两点。
轴向上平移3个单位长度后恰好经过B、C两点。
(1)求直线BC及抛物线的解析式;
(2)设抛物线的顶点为D,点P在抛物线的对称轴上,且 ,求点P的坐标。
,求点P的坐标。
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
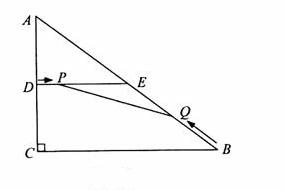
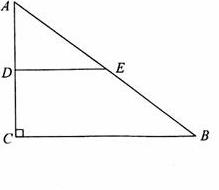
已知:如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,D、E分别是AC、AB的中点,连接DE,点P从点D出发,沿DE方向匀速运动,速度为1cm/s;同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(s)(0<t<4).解答下列问题:
⑴当t为何值时,PQ⊥AB?
(2)当点Q在BE之间运动时,是否存在某一时刻t,使PQ分四边形BCDE两部分的面积之比为S△PQE:S五边形PQBCD=1:29?若存在,求出此时t的值以及点E到PQ的距离h;若不存在,请说明理由。
(3)在P、Q运动过程中,当t为何值时,△PEQ为等腰三角形?
 |  |
查看答案和解析>>
科目:初中数学 来源: 题型:
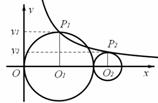
如图,平面直角坐标系中,⊙O1过原点O,且⊙O1与⊙O2相外切,圆心O1与O2在x轴正半轴上,⊙O1的半径O1P1、⊙O2的半径O2P2都与x轴垂直,且点P1 、P2
、P2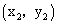 在反比例函数
在反比例函数 (x>0)的图象上,则
(x>0)的图象上,则 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
在直角梯形ABCD中,AD∥BC,∠B=∠A=90°.
操作示例
小明取直角梯形ABCD的非直角腰CD的中点P,过点P作PE∥AB,剪下△PEC(如图1),并将△PEC绕点P按逆时针方向旋转180°到△PFD的位置,拼成新的图形(如图2).
(Ⅰ)思考与实践:
(1)操作后小明发现,拼成的新图形是矩形,请帮他说明理由;
 (2)如图3四边形ABCD中AB∥CD,请你类比图2的剪拼方法,在图3画出剪拼成一个平行四边形的示意图.
(2)如图3四边形ABCD中AB∥CD,请你类比图2的剪拼方法,在图3画出剪拼成一个平行四边形的示意图.
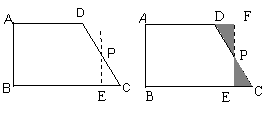 |
图1 图2
(Ⅱ)发现与运用:
|
请你选择下面两题中的一题作答:(多做不加分,两题都做按第一题计分)
(1)如图4,在梯形ABCD中,AD∥BC,E是CD的中点, EF⊥AB于点F,AB=5,EF=4,求梯形ABCD的面积。
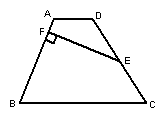
图4
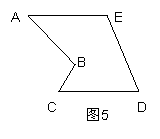
(2)如图4的多边形中,AE=CD,AE∥CD,能否沿一条直线进行剪切,拼成一个平行四边形?若能,请你在图中画出剪拼的示意图并作必要的文字说明;若不能,简要说明理由.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E,B、E是半圆弧的三等分点,弧BE的长为 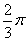 ,则图中阴影部分的面积为……( )
,则图中阴影部分的面积为……( )
A.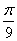 B.
B. 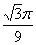 C.
C.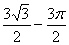 D.
D.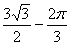
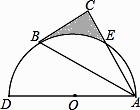
(第9题)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com