
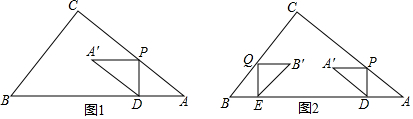
���� ��1�����ݹ��ɶ������AC��֤����APD�ס�ABC����A��PC�ס�ABC���������������ε����ʼ��㣻
��2����A��B=BC��A��B=A��C������������ݵ��������ε����ʽ��
��3���������⻭��ͼ�Σ�����������Ǻ����ĸ�����㣮
���  �⣺��1����ͼ1�����ڡ�ABC�У���C=90�㣬AB=5cm��BC=3cm��
�⣺��1����ͼ1�����ڡ�ABC�У���C=90�㣬AB=5cm��BC=3cm��
��AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4cm��
����A�����ڱ�BC��ʱ��������ã��ı���APA��DΪƽ���ı��Σ�
��PD��AB��
���ADP=��C=90�㣬
�ߡ�A=��A��
���APD�ס�ABC��
��AP=5x��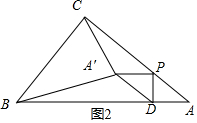
��A��P=AD=4x��PC=4-5x��
�ߡ�A��PD=��ADP��
��A��P��AB��
���A��PC�ס�ABC��
��$\frac{PC}{AC}=\frac{A��P}{AB}$����$\frac{4-5x}{4}$=$\frac{4x}{5}$��
��ã�x=$\frac{20}{41}$��
�൱��A�����ڱ�BC��ʱ��x=$\frac{20}{41}$��
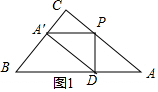
��2����A��B=BCʱ����5-8x��2+��3x��2=32��
��ã�$x=\frac{{40��12\sqrt{3}}}{73}$��
��x��$\frac{4}{5}$��
��$x=\frac{{40-12\sqrt{3}}}{73}$��
��A��B=A��Cʱ��x=$\frac{5}{8}$��
��3����A��B���ABʱ����ͼ6��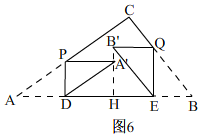 ��DH=PA'=AD��HE=B��Q=EB��
��DH=PA'=AD��HE=B��Q=EB��
��AB=2AD+2EB=2��4x+2��3x=5��
��x=$\frac{5}{14}$��
��A��B��=QE-PD=x=$\frac{5}{14}$��
��A��B���BCʱ����ͼ7��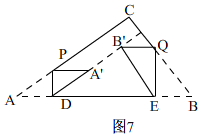 ��B��E=5x��DE=5-7x��
��B��E=5x��DE=5-7x��
��cosB=$\frac{5x}{5-7x}=\frac{3}{5}$��
��x=$\frac{15}{46}$��
��A��B��=B��D-A��D=$\frac{25}{23}$��
��A��B���ACʱ����ͼ8��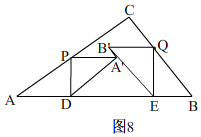 �ɣ�1���У�x=$\frac{20}{41}$��
�ɣ�1���У�x=$\frac{20}{41}$��
��A��B��=PA��sinA=$\frac{12}{41}$��
��A��B���ABʱ��x=$\frac{5}{14}$��A��B��=$\frac{5}{14}$��
��A��B���BCʱ��x=$\frac{15}{46}$��A��B��=$\frac{25}{23}$��
��A��B���ACʱ��x=$\frac{20}{41}$��A��B��=$\frac{12}{41}$��
���� �����Ǽ��α任�ۺ��⣬��Ҫ������������Ǻ��������壬�������ۣ��Ȿ��Ĺؼ���Ҫ����Ҫ�����ѵ��Ƿ��࣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{8}$ | B�� | $\frac{1}{6}$ | C�� | $\frac{3}{8}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
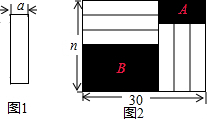 ��������״��С��ȫ��ͬ��С�����ο�Ƭ�����н϶̵�һ�߳�Ϊa���ף���ͼ1�����ص��ط���һ������Ϊ�����Σ���Ϊ30cm����Ϊncm���ĺ��ӵײ�����ͼ2�������ӵ���δ����Ƭ���ǵIJ��ֱַ���A��B��ʾ����۲�ͼ�Σ��ش����⣺
��������״��С��ȫ��ͬ��С�����ο�Ƭ�����н϶̵�һ�߳�Ϊa���ף���ͼ1�����ص��ط���һ������Ϊ�����Σ���Ϊ30cm����Ϊncm���ĺ��ӵײ�����ͼ2�������ӵ���δ����Ƭ���ǵIJ��ֱַ���A��B��ʾ����۲�ͼ�Σ��ش����⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �ۼۣ�Ԫ/���� | 100 | 110 | 120 | 130 | �� |
| ������������ | 200 | 180 | 160 | 140 | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
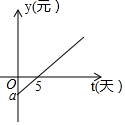 ij���߲��г��������¾�Ӫģʽ�������߲˾�Ӫ�����г�������������̯λ��ÿ�½���һ���ġ�̯λ�ѡ������г������ȷ��ã����߲��г�������˾����ÿ���ġ�̯λ�ѡ�ӯ�������徭Ӫ��ÿ��Ӫһ�죬ƽ���ɵá�Ӫҵ�800Ԫ����ƽ��ÿ��Ҫ֧���߲˵ġ������ѡ�400Ԫ����ͼ��ij�����߲˾�Ӫ�̾�Ӫһ���£�����30����㣩�����棨��ȥ��̯λ�ѡ��͡������ѡ���yԪ�澭Ӫʱ��t��仯�ĺ���ͼ��
ij���߲��г��������¾�Ӫģʽ�������߲˾�Ӫ�����г�������������̯λ��ÿ�½���һ���ġ�̯λ�ѡ������г������ȷ��ã����߲��г�������˾����ÿ���ġ�̯λ�ѡ�ӯ�������徭Ӫ��ÿ��Ӫһ�죬ƽ���ɵá�Ӫҵ�800Ԫ����ƽ��ÿ��Ҫ֧���߲˵ġ������ѡ�400Ԫ����ͼ��ij�����߲˾�Ӫ�̾�Ӫһ���£�����30����㣩�����棨��ȥ��̯λ�ѡ��͡������ѡ���yԪ�澭Ӫʱ��t��仯�ĺ���ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
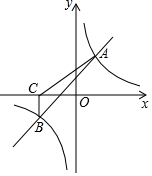 ��ͼ��һ�κ���y=kx+b�뷴��������y=$\frac{m}{x}$��ͼ����A��2��3����
��ͼ��һ�κ���y=kx+b�뷴��������y=$\frac{m}{x}$��ͼ����A��2��3�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2a3��a=6 | B�� | ��a+b����a-b��=a2-b2 | C�� | ��ab3��2=a2b5 | D�� | ��a+b��2=a2+b2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com