练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．已知（x-15）2+$\sqrt{17-y}$+z2-16z+64=0，试判断以x，y，z为三边的三角形的形状．

    分析 先根据非负数的性质求出x、y、z的值，再根据勾股定理的逆定理进行解答即可．

    解答 解：以x，y，z为三边的三角形是直角三角形．
    ∵（x-15）2+$\sqrt{17-y}$+z2-16z+64=0，
    ∴（x-15）2+$\sqrt{17-y}$+（z-8）2=0，
    ∴x-15=0，17-y=0，z-8=0，
    ∴x=15，y=17，z=8，
    ∵152+82=172，
    ∴以x，y，z为三边的三角形是直角三角形．

    点评 本题考查的是勾股定理的逆定理，熟知如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．已知：y=$\sqrt{1-8x}+\sqrt{8x-1}$+$\frac{1}{2}$，求代数式$\sqrt{\frac{x}{y}+\frac{y}{x}+2}-\sqrt{\frac{x}{y}+\frac{y}{x}-2}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

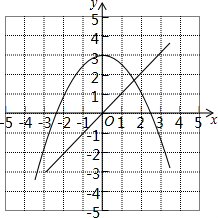    1．我们在求方程x2+2x-6=0的近似根时，可以将原方程变形为-$\frac{1}{2}$x2+3=x，然后在同一直角坐标系中画出函数y=-$\frac{1}{2}$x2+3和y=x的图象，发现-4＜x1＜-3，1＜x2＜2．请你利用已有的函数图象判断方程x3-6x+12=0在实数范围内有几个解？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．若分式$\frac{3}{{x}^{2}-2x+m}$不论x取何实数都有意义，则m的取值范围是m＞1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．用反证法证明命题“如果a＞b，那么$\root{3}{a}＞\root{3}{b}$”时，假设的内容是$\root{3}{a}$＜$\root{3}{b}$或$\root{3}{a}$=$\root{3}{b}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．在△ABC中，∠ACB=45°．点D（与点B、C不重合）为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．
    （1）如果AB=AC，如图①，且点D在线段BC上运动，试判断线段CF与BD之间的位置关系，并证明你的结论；
    （2）如果AB＞AC，如图②，且点D在线段BC上运动，（1）中结论是否成立，说明理由．
    （3）如果AB＜AC，如图③，且正方形ADEF的边DE所在直线与线段CF所在直线相交于点P，设AC=4$\sqrt{2}$，BC=3，CD=x，求线段CP的长．（用含x的式子表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．若整数x，y，z满足方程组$\left\{\begin{array}{l}{xy+z=94}\\{x+yz=95}\end{array}\right.$，则xyz=1984或0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

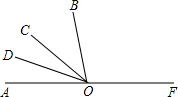    7．如图，已知O为直线AF上一点，射线OC平分∠AOB，∠COD=20°；
    （1）若∠AOB=80°，试说明OD为∠AOC的角平分线；
    （2）若∠BOD=60°，求∠COF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．在半径为2的圆中，扇形AOB的圆心角为120°，则这个扇形面积为$\frac{4}{3}$π．

    查看答案和解析>>

    同步练习册答案