
| x | … | -1 | 0 | 3 | … |
| y1=ax2+bx+c | … | 0 |  | 0 | … |
 解:(Ⅰ)∵抛物线经过点(0,
解:(Ⅰ)∵抛物线经过点(0, ),
), .
. ,
, 上,
上,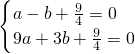 ,解得
,解得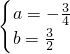 ,
, x2+
x2+ x+
x+ ;
; x2+
x2+ x+
x+ ,
, (x-1)2+3,
(x-1)2+3,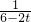 (x-1)2+
(x-1)2+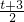 ,
,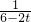 x2-
x2-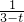 x+
x+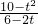 ,
,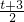 ),
),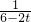 x2-
x2-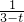 x+
x+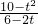 (t≠3);
(t≠3);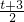 ),
),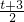 ,
, (x-1)2+3-[
(x-1)2+3-[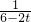 (x-1)2+
(x-1)2+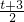 ]
]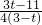 (x-1)2+
(x-1)2+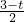 ,
,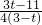 (x-1)2+
(x-1)2+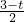 开口方向向下,且顶点(1,
开口方向向下,且顶点(1,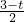 )在x轴下方,
)在x轴下方, ,符合题意;
,符合题意; <0,即t=
<0,即t= 也符合题意.
也符合题意. .
. )得出c的值,再把点(-1,0)、(3,0)代入抛物线y1的解析式即可得出y1与x之间的函数关系式;
)得出c的值,再把点(-1,0)、(3,0)代入抛物线y1的解析式即可得出y1与x之间的函数关系式;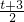 ),由于3>
),由于3>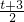 ,所以不合题意,当抛物线y2开口方向向下时,6-2t<0,即t>3时,求出y1-y2的值;若3t-11≠0,要使y1<y2恒成立,只要抛物线方向及且顶点(1,
,所以不合题意,当抛物线y2开口方向向下时,6-2t<0,即t>3时,求出y1-y2的值;若3t-11≠0,要使y1<y2恒成立,只要抛物线方向及且顶点(1,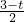 )在x轴下方,因为3-t<0,只要3t-11>0,解得t>
)在x轴下方,因为3-t<0,只要3t-11>0,解得t> ,符合题意;若3t-11=0,y1-y2=-
,符合题意;若3t-11=0,y1-y2=- <0,即t=
<0,即t= 也符合题意.
也符合题意.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 9 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
 ,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值?
,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值?查看答案和解析>>
科目:初中数学 来源: 题型:044
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设A(x1,y1)、B(x2,y2)是抛物线与直线的两个交点,点P是线段AB的中点,且点P的横坐标为![]() ,试用含a的代数式表示点P的纵坐标;
,试用含a的代数式表示点P的纵坐标;
(3)设A,B两点的距离d=![]() ·|x1-x2|,试用含a的代数式表示d.
·|x1-x2|,试用含a的代数式表示d.
查看答案和解析>>
科目:初中数学 来源:2008年江西省中考数学试卷(解析版) 题型:解答题
 时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com