
| A. | 2013 | B. | 2014 | C. | 2015 | D. | 2016 |
科目:初中数学 来源: 题型:选择题
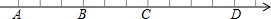 如图,数轴上每相邻两点相距一个单位长度,点A、B、C、D对应的位置如图所示,它们对应的数分别是a、b、c、d,且d-b+c=10,那么点A对应的数是( )
如图,数轴上每相邻两点相距一个单位长度,点A、B、C、D对应的位置如图所示,它们对应的数分别是a、b、c、d,且d-b+c=10,那么点A对应的数是( )| A. | -6 | B. | -3 | C. | 0 | D. | 正数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
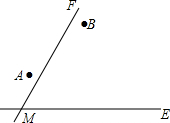 两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部
两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=ax2+bx-3与x轴交于A、B两点,与y轴交于点C,O是坐
如图,已知抛物线y=ax2+bx-3与x轴交于A、B两点,与y轴交于点C,O是坐查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15 | B. | 14 | C. | 13 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源:2017届湖北省襄阳老河口九年级3月月考数学试卷(解析版) 题型:判断题
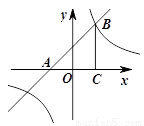
如图所示,一次函数y1=x+1的图象与x轴交于点A,与反比例函数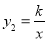 的图象在第一象限内交于点B,作BC⊥x轴,垂足为C,且OC=1.
的图象在第一象限内交于点B,作BC⊥x轴,垂足为C,且OC=1.
(1)请直接写出在第一象限内,当x取何值时,y1>y2?
(2)将线段BC沿一次函数的图象平移至点B与点A重合,平移后点C的对应点是否在反比例函数的图象上?
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
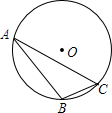 如图,⊙O的半径是1,A、B、C是圆周上的三点,∠BAC=36°,则弦BC所对的弧长是$\frac{2}{5}$π或$\frac{8}{5}$π.
如图,⊙O的半径是1,A、B、C是圆周上的三点,∠BAC=36°,则弦BC所对的弧长是$\frac{2}{5}$π或$\frac{8}{5}$π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com