
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.
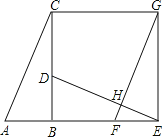
(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
【答案】(1)FG⊥ED;(2)见解析
【解析】
试题分析:(1)根据旋转和平移可得∠DEB=∠ACB,∠GFE=∠A,再根据∠ABC=90°可得∠A+∠ACB=90°,进而得到∠DEB+∠GFE=90°,从而得到DE、FG的位置关系是垂直;
(2)根据旋转和平移找出对应线段和角,然后再证明是矩形,后根据邻边相等可得四边形CBEG是正方形.
(1)解:FG⊥ED.理由如下:
∵△ABC绕点B顺时针旋转90°至△DBE后,
∴∠DEB=∠ACB,
∵把△ABC沿射线平移至△FEG,
∴∠GFE=∠A,
∵∠ABC=90°,
∴∠A+∠ACB=90°,
∴∠DEB+∠GFE=90°,
∴∠FHE=90°,
∴FG⊥ED;
(2)证明:根据旋转和平移可得∠GEF=90°,∠CBE=90°,CG∥EB,CB=BE,
∵CG∥EB,
∴∠BCG=∠CBE=90°,
∴四边形BCGE是矩形,
∵CB=BE,
∴四边形CBEG是正方形.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD.
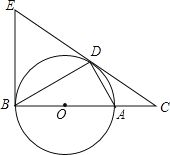
(1)求证:CD是⊙O的切线;
(2)过点B作O的切线,交CD的延长线于点E,若BC=12,tan∠CDA=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
种子粒数 | 100 | 400 | 800 | 1000 | 2000 | 5000 |
发芽种子粒数 | 85 | 318 | 652 | 793 | 1604 | 4005 |
发芽频率 | 0.850 | 0.795 | 0.815 | 0.793 | 0.802 | 0.801 |
根据以上数据可以估计,该玉米种子发芽的概率约为(精确到0.10).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A.两组对边分别相等的四边形是平行四边形
B.对角线相等的平行四边形是矩形
C.对角线垂直的平行四边形是菱形
D.四条边相等的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.

(1)求证:BE=CE;
(2)以点E为圆心,ED长为半径画弧,分别交BE,CE于点F,G.若BC=4,EB平分∠ABC,求图中阴影部分(扇形)的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com