
已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于C点,与x轴交于A、B两点,A点在B点左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD的面积的最大值;
(3)若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?若存在,求点P的坐标;若不存在,请说明理由.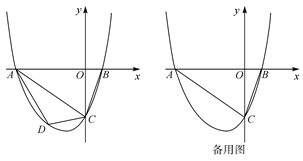
(1)∴y= x2+
x2+ x-3
x-3
(2)过点D作DM∥y轴分别交线段AC和x轴于点M、N.
∴S四边形ABCD=S△ABC+S△ACD= +
+ ·DM·(AN+ON)=
·DM·(AN+ON)= +2DM.
+2DM.
∵A(-4,0),C(0,-3),
设直线AC的解析式为y=kx+b,
代入求得:y=- x-3,
x-3,
令D ,M
,M ,
,
则DM=- x-3-
x-3- =-
=- (x+2)2+3.
(x+2)2+3.
当x=-2时,DM有最大值3,此时四边形ABCD面积有最大值 .
.
(3)如图①所示,讨论:①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形,
∵C(0,-3),令 x2+
x2+ x-3=-3得x1=0,x2=-3,
x-3=-3得x1=0,x2=-3,
∴CP1=3.∴P1(-3,-3).
②如图②,平移直线AC交x轴于点E,交x轴上方的抛物线于点P,
当AC=PE时,四边形ACEP为平行四边形,
∵C(0,-3),
∴可令P(x,3),由 x2+
x2+ x-3=3得:x2+3x-8=0,
x-3=3得:x2+3x-8=0,
解得x1= 或x2=
或x2= ,
,
此时存在点P2 和P3
和P3 .
.
综上所述,存在3个点符合题意,坐标分别是P1(-3,-3),P2 ,P3
,P3 .
.
解析


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源:2009年福建莆田初中毕业、升学统一考试数学试卷及答案 题型:044
已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于C点,与x轴交于A、B两点,A点在B点左侧.点B的坐标为(1,0),OC=30B.
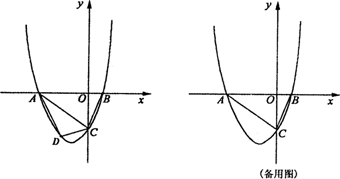
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值:
(3)若点E在x轴上,点P在抛物线上.是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,等腰梯形ABCD的边BC在x轴上,点A在y轴的正方向上,A( 0, 6 ),D ( 4,6),且AB=![]() .
.
⑴求点B的坐标;
⑵求经过A、B、D三点的抛物线的解析式;
⑶在⑵中所求的抛物线上是否存在一点P,使得S△PBC = ![]() S梯形ABCD?若存在,请求出该点坐标,若不存在,请说明理由.
S梯形ABCD?若存在,请求出该点坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2012-2013学年四川成都望子成龙学校九年级上期中数学试卷(解析版) 题型:解答题
已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于C点,与x轴交于A、B两点,A点在B点左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD的面积的最大值;
(3)若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(湖南衡阳卷)数学 题型:解答题
已知:如图9,等腰梯形ABCD的边BC在x轴上,点A在y轴的正方向上,A( 0, 6 ),D ( 4,6),且AB=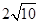 .
.
(1)求点B的坐标;
(2)求经过A、B、D三点的抛物线的解析式;
(3)在(2)中所求的抛物线上是否存在一点P,
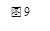 使得
使得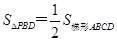 ?若存在,请求出该点坐标,
?若存在,请求出该点坐标,
若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com