
分析 先利用tanα=$\frac{sinα}{cosα}$得到原式=$\frac{3sinα-\frac{sinα}{cosα}}{4sinα+2\frac{sinα}{cosα}}$=$\frac{3cosα-1}{4cosα+2}$,然后把cosα=$\frac{1}{3}$代入计算即可.
解答 解:∵tanα=$\frac{sinα}{cosα}$,
∴$\frac{3sinα-tanα}{4sinα+2tanα}$=$\frac{3sinα-\frac{sinα}{cosα}}{4sinα+2\frac{sinα}{cosα}}$=$\frac{3cosα-1}{4cosα+2}$,
∵cosα=$\frac{1}{3}$,
∴$\frac{3sinα-tanα}{4sinα+2tanα}$=$\frac{3×\frac{1}{3}-1}{4×\frac{1}{3}+2}$=0.
故答案为0.
点评 本题考查了同角三角函数的关系:平方关系:sin2A+cos2A=1;正余弦与正切之间的关系(积的关系):一个角的正切值等于这个角的正弦与余弦的比,即tanA=$\frac{sinA}{cosA}$或sinA=tanA•cosA.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:选择题
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
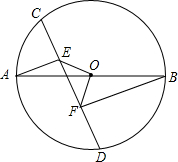 如图:在⊙O中,AB是直径,CD是弦,$\widehat{AD}$=$\widehat{BD}$,过点A、B两点分别作CD的垂线,垂足分别是点E、F.连接OE,OF,求证:△OEF是等腰直角三角形.
如图:在⊙O中,AB是直径,CD是弦,$\widehat{AD}$=$\widehat{BD}$,过点A、B两点分别作CD的垂线,垂足分别是点E、F.连接OE,OF,求证:△OEF是等腰直角三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com