
【题目】如图,四边形ABCD、DEFG都是正方形,AB与CG交于点![]() 下列结论:
下列结论:![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() 其中正确的有______;
其中正确的有______;

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.

解答下面的问题:
(1)求过点P(1,4)且与已知直线y=-2x-1平行的直线的函数表达式,并画出直线l的图象;
(2)设直线l分别与y轴、x轴交于点A、B,如果直线![]() :y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
:y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F;再分别以点E、F为圆心,大于 ![]() EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )
EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( ) 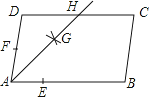
A.AG平分∠DAB
B.AD=DH
C.DH=BC
D.CH=DH
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知 P是线段 AB上的一点,![]() ,C, D两点从 A, P同时出发,分别以2
,C, D两点从 A, P同时出发,分别以2 ![]() ,1
,1![]() 的速度沿 AB方向运动,当点 D到达终点 B时,点C也停止运动,设AB=
的速度沿 AB方向运动,当点 D到达终点 B时,点C也停止运动,设AB=![]()
![]() ,点 C,D的运动时间为
,点 C,D的运动时间为![]() .
.
(1)用含![]() 和 的代数式表示线段 CP 的长度.
和 的代数式表示线段 CP 的长度.
(2)当 t =5时,![]() ,求线段 AB的长.
,求线段 AB的长.
(3)当 BC-AC=PC时,求 ![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.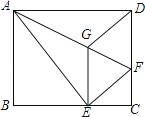
(1)求证:四边形EFDG是菱形;
(2)探究线段EG、GF、AF之间的数量关系,并说明理由;
(3)若AG=6,EG=2 ![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=120°,AB=AC,∠ACB的平分线交AB于D,AE平分∠BAC交BC于E,连接DE,DF⊥BC于F,则∠EDC=_____°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点C,与y轴交于点B,点A(1,3),点B(0,2).连接AO
(1)求直线AB的解析式;
(2)求三角形AOC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com