
【题目】如图,直线AB与x轴交于点C,与y轴交于点B,点A(1,3),点B(0,2).连接AO
(1)求直线AB的解析式;
(2)求三角形AOC的面积.

【答案】(1) y=x+2;(2)3.
【解析】
(1)设直线AB的解析式为y=kx+b,把A、B的坐标代入求出k、b的值即可,
(2)把y=0代入(1)所求出的解析式,便能求出C点坐标,从而利用三角形的面积公式求出三角形AOC的面积即可.
(1)设直线AB的解析式y=kx+b,
把点A(1,3),B(0,2)代入解析式得:![]() ,
,
解得:k=1,b=2,
把k=1,b=2代入y=kx+b得:y=x+2,
直线AB的解析式:y=x+2;
(2)把 y=0代入y=x+2得:x+2=0,
解得:x=﹣2,
∴点C的坐标为(﹣2,0),
∴OC=2,
∵△AOC的底为2,△AOC的高为点A的纵坐标3,
∴S△ABC=2×3×![]() =3,
=3,
故三角形AOC的面积为3.


科目:初中数学 来源: 题型:
【题目】如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y= ![]() 上(k>0,x>0),则k的值为( )
上(k>0,x>0),则k的值为( )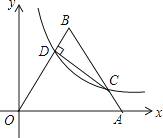
A.25 ![]()
B.18 ![]()
C.9 ![]()
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=3EQ;④△PBF是等边三角形,其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=3EQ;④△PBF是等边三角形,其中正确的是( )

A. ①②③ B. ②③④ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2017个小正方形,则需要操作的次数是( )
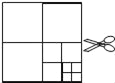
A. 672 B. 671 C. 670 D. 674
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】OC把∠AOB分成两部分且有下列两个等式成立:
①∠AOC=![]() 直角+
直角+![]() ∠BOC;②∠BOC=
∠BOC;②∠BOC=![]() 平角-
平角-![]() ∠AOC,问∶
∠AOC,问∶
(1)OA与OB的位置关系怎样?
(2)OC是否为∠AOB的平分线?并写出判断的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠B=∠C.
(1)若AD∥BC,则AD平分∠EAC吗?请说明理由.
(2)若∠B+∠C+∠BAC=180°,AD平分∠EAC,则AD∥BC吗?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com