
 =
=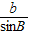 =
= =2R.
=2R. =
= ,
, ,即
,即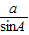 =2R,
=2R, =2R,
=2R, =2R,
=2R, =
= =
= =2R,
=2R, =2R,
=2R, =2R”的证明过程,请你把“
=2R”的证明过程,请你把“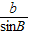 =2R”的证明过程补写出来.
=2R”的证明过程补写出来. ,CA=
,CA= ,∠A=60°,求△ABC的外接圆半径R及∠C.
,∠A=60°,求△ABC的外接圆半径R及∠C.

科目:初中数学 来源: 题型:
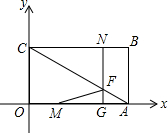 在平面直角坐标系中,已知两点坐标P1(x1,y1)P2(x2,y2)我们就可以使用两点间距离公式P1P2=
在平面直角坐标系中,已知两点坐标P1(x1,y1)P2(x2,y2)我们就可以使用两点间距离公式P1P2=| (x1-x2)2+(y1-y 2)2 |
| (-1-0)2+(2-3)2 |
| 2 |
| 13 |
| 13 |
| 13 |
| 13 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《二次函数》(04)(解析版) 题型:解答题
 ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2002年辽宁省大连市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2002年广东省深圳市中考数学试卷(解析版) 题型:解答题
 =
= =
= =2R.
=2R. =
= ,
, ,即
,即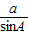 =2R,
=2R, =2R,
=2R, =2R,
=2R, =
= =
= =2R,
=2R, =2R,
=2R, =2R”的证明过程,请你把“
=2R”的证明过程,请你把“ =2R”的证明过程补写出来.
=2R”的证明过程补写出来. ,CA=
,CA= ,∠A=60°,求△ABC的外接圆半径R及∠C.
,∠A=60°,求△ABC的外接圆半径R及∠C.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com