
 如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )
如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )| A. | x-y2=3 | B. | 2x-y2=9 | C. | 3x-y2=15 | D. | 4x-y2=21 |
分析 过A作AQ⊥BC于Q,过E作EM⊥BC于M,连接DE,根据线段垂直平分线求出DE=BD=x,根据等腰三角形求出BD=DC=6,求出CM=DM=3,解直角三角形求出EM=3y,AQ=6y,在Rt△DEM中,根据勾股定理求出即可.
解答 解: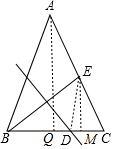
过A作AQ⊥BC于Q,过E作EM⊥BC于M,连接DE,
∵BE的垂直平分线交BC于D,BD=x,
∴BD=DE=x,
∵AB=AC,BC=12,tan∠ACB=y,
∴$\frac{EM}{MC}$=$\frac{AQ}{CQ}$=y,BQ=CQ=6,
∴AQ=6y,
∵AQ⊥BC,EM⊥BC,
∴AQ∥EM,
∵E为AC中点,
∴CM=QM=$\frac{1}{2}$CQ=3,
∴EM=3y,
∴DM=12-3-x=9-x,
在Rt△EDM中,由勾股定理得:x2=(3y)2+(9-x)2,
即2x-y2=9,
故选B.
点评 本题考查了线段垂直平分线性质,等腰三角形的性质,勾股定理,解直角三角形等知识点,能正确作出辅助线是解此题的关键.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{10}$ | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | -8 | C. | $\frac{1}{8}$ | D. | $-\frac{1}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶点A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是13米,梯坎坡度i=1:2.4,则大楼AB的高度约为( )
如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶点A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是13米,梯坎坡度i=1:2.4,则大楼AB的高度约为( )| A. | 40 | B. | 41 | C. | 42 | D. | 47 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
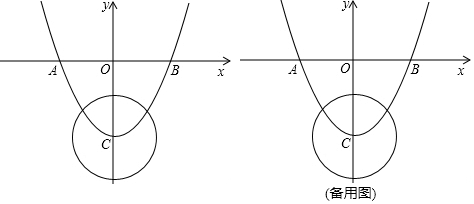
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
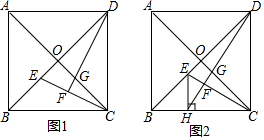
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
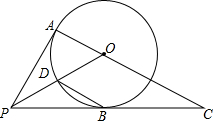 如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.
如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.查看答案和解析>>
科目:初中数学 来源:2017届江苏省启东市九年级寒假作业测试(开学考试)数学试卷(解析版) 题型:解答题
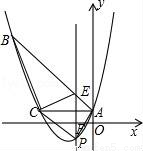
如图,已知抛物线y=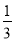 x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com