
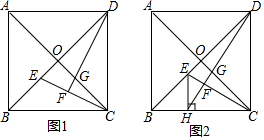
分析 (1)欲证明OE=OG,只要证明△DOG≌△COE(ASA)即可;
(2)①欲证明∠ODG=∠OCE,只要证明△ODG≌△OCE即可;
②设CH=x,由△CHE∽△DCH,可得$\frac{EH}{HC}$=$\frac{HC}{CD}$,即HC2=EH•CD,由此构建方程即可解决问题;
解答 (1)证明:如图1中,∵四边形ABCD是正方形,
∴AC⊥BD,OD=OC,
∴∠DOG=∠COE=90°,
∴∠OEC+∠OCE=90°,
∵DF⊥CE,
∴∠OEC+∠ODG=90°,
∴∠ODG=∠OCE,
∴△DOG≌△COE(ASA),
∴OE=OG.
(2)①证明:如图2中,∵OG=OE,∠DOG=∠COE=90°OD=OC,
∴△ODG≌△OCE,
∴∠ODG=∠OCE.
②解:设CH=x,
∵四边形ABCD是正方形,AB=1,
∴BH=1-x,∠DBC=∠BDC=∠ACB=45°,
∵EH⊥BC,
∴∠BEH=∠EBH=45°,
∴EH=BH=1-x,
∵∠ODG=∠OCE,
∴∠BDC-∠ODG=∠ACB-∠OCE,
∴∠HDC=∠ECH,
∵EH⊥BC,
∴∠EHC=∠HCD=90°,
∴△CHE∽△DCH,
∴$\frac{EH}{HC}$=$\frac{HC}{CD}$,
∴HC2=EH•CD,
∴x2=(1-x)•1,
解得x=$\frac{\sqrt{5}-1}{2}$或$\frac{-\sqrt{5}-1}{2}$(舍弃),
∴HC=$\frac{\sqrt{5}-1}{2}$.
点评 本题考查正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 8.05×10-8 | B. | 8.05×10-7 | C. | 80.5×10-9 | D. | 0.805×10-7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )
如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )| A. | x-y2=3 | B. | 2x-y2=9 | C. | 3x-y2=15 | D. | 4x-y2=21 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
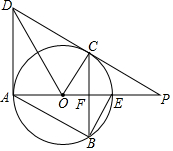 如图所示,直线DP和圆O相切于点C,交直径AE的延长线于点P.过点C作AE的垂线,交AE于点F,交圆O于点B.作平行四边形ABCD,连接BE,DO,CO.
如图所示,直线DP和圆O相切于点C,交直径AE的延长线于点P.过点C作AE的垂线,交AE于点F,交圆O于点B.作平行四边形ABCD,连接BE,DO,CO.查看答案和解析>>
科目:初中数学 来源:2017届江苏省启东市九年级寒假作业测试(开学考试)数学试卷(解析版) 题型:填空题
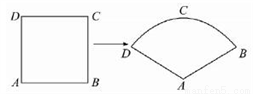
如图,某数学兴趣小组将边长为5的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com