在数学活动课上，小明提出这样一个问题：如图，∠B＝∠C＝90°，E是BC的中点，DE平分∠ADC，∠CED＝35°，则∠EAB的度数是（ ）
A. 65° B. 55° C. 45° D. 35°
通城学典默写能手系列答案科目：初中数学 来源：山东省青岛市2019届九年级北师大版上册期中检测试卷数学试卷 题型：解答题
请阅读下列材料：
问题：如图，在正方形
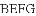
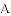
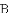
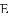
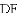
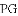
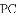
探究：当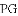
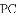
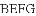
小聪同学的思路是：首先可以说明四边形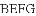
请你参考小聪同学的思路，探究并解决这个问题．
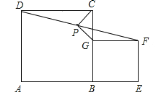
（1）求证：四边形
（2）
理由：
查看答案和解析>>
科目：初中数学 来源：北师大新版数学九年级上学期《第3章概率的进一步认识》单元测试 题型：解答题
某工厂甲、乙两个部门各有员工400人，为了解这两个部门员工的生产技能情况，进行了抽样调查，过程如下，请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工，进行了生产技能测试，测试成绩（百分制）如下：
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据：
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
（说明：成绩80分及以上为生产技能优秀，70--79分为生产技能良好，60--69分为生产技能合格，60分以下为生产技能不合格）
分析数据
两组样本数据的平均数、中位数、众数如下表所示：
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | 75 |
乙 | 78 | 80.5 | 81 |
得出结论：
.估计乙部门生产技能优秀的员工人数为____________；
.可以推断出_____________部门员工的生产技能水平较高，理由为_____________.（至少从两个不同的角度说明推断的合理性）
查看答案和解析>>
科目：初中数学 来源：北师大新版数学九年级上学期《第3章概率的进一步认识》单元测试 题型：单选题
从3、1、－2这三个数中任取两个不同的数作为P点的坐标，则P点刚好落在第四象限的概率是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源：江苏省无锡市2018-2019学年七年级10月月考数学试卷 题型：解答题
（阅读理解）
点A、B、C为数轴上三点，如果点C在A、B之间且到A的距离是点C到B的距离3倍，那么我们就称点C是{ A，B }的奇点．
例如，如图1，点A表示的数为﹣3，点B表示的数为1．表示0的点C到点A的距离是3，到点B的距离是1，那么点C是{ A，B }的奇点；又如，表示﹣2的点D到点A的距离是1，到点B的距离是3，那么点D就不是{A，B }的奇点，但点D是{B，A}的奇点．
（知识运用）
如图2，M、N为数轴上两点，点M所表示的数为﹣3，点N所表示的数为5．
（1）数 所表示的点是{ M，N}的奇点；数 所表示的点是{N，M}的奇点；
（2）如图3，A、B为数轴上两点，点A所表示的数为﹣50，点B所表示的数为30．现有一动点P从点B出发向左运动，到达点A停止．P点运动到数轴上的什么位置时，P、A和B中恰有一个点为其余两点的奇点？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
B. 
C. 
D. 
（2） 
的结果是_____．
B. 
C. 
D. 
