
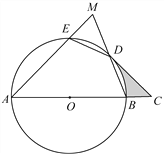
【题目】如图,AB是⊙O的直径,![]() ,连接ED,BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
,连接ED,BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
(1)若OA=CD=2![]() ,求阴影部分的面积;
,求阴影部分的面积;
(2)求证:DE=DM.
【答案】(1)4-π(2)证明见解析
【解析】
试题(1)连接OD,由已知条件可证出三角形ODC是等腰直角三角形,OD的长度知道,∠DOB的度数是45度,这样,阴影的面积就等于等腰直角三角形ODC的面积减去扇形ODB的面积;
(2)连接AD,由已知条件可证出AD垂直平分BM,从而得到DM=DB,又因为弧DE=弧DB,DE=DB,所以DE就等于DM.
试题解析:(1)连接OD,
∵CD是⊙O切线,
∴OD⊥CD∵OA=CD =![]() ,
,
OA=OD∴OD=CD=![]()
∴△OCD 为等腰直角三角形∠DOC=∠C=45°
S阴影=S△OCD-S扇OBD=![]() ×
×![]() ×
×![]() -
-![]() =4-π;
=4-π;
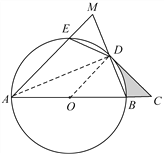
(2)连接AD.
∵AB是⊙O直径
∴∠ADB=∠ADM= 90°
又∵弧ED=弧BD
∴ED=BD ∠MAD=∠BAD
∴△AMD≌△ABD
∴DM=BD
∴DE=DM.


科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里有1个红球,1个黄球和n个白球,它们除颜色外其余都相同.
(1)从这个袋子里摸出一个球,记录其颜色,然后放回,摇均匀后,重复该实验,经过大量实验后,发现摸到白球的频率稳定于0.5左右,求n的值;
(2)在(1)的条件下,先从这个袋中摸出一个球,记录其颜色,放回,摇均匀后,再从袋中摸出一个球,记录其颜色.请用画树状图或者列表的方法,求出先后两次摸出不同颜色的两个球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了15人某月的加工零件个数:
每人加工件数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数。
(2)若以本次统计所得的月加工零件数的平均数定为每位工人每月的生产定额,你认为这个定额是否合理,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
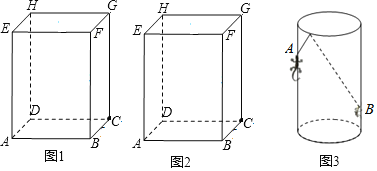
【题目】(1)如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;
(2)如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程.
(3)若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=![]() ,且经过点(2,0),有下列说法:①abc>0;②a+b=0;③4a+2b+c <0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
,且经过点(2,0),有下列说法:①abc>0;②a+b=0;③4a+2b+c <0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
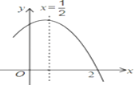
A. ①②④ B. ②④ C. ①③④ D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
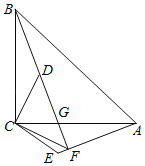
【题目】如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.
(1)求证:△ACE≌△BCD;
(2)求证:BF⊥AE;
(3)请判断∠CFE与∠CAB的大小关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
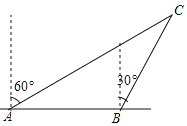
【题目】如图,某渔船向正东方向以12海里/时的速度航行,在A处测得岛C在北偏东的60°方向,1小时后渔船航行到B处,测得岛C在北偏东的30°方向,已知该岛周围10海里内有暗礁.
(1)B处离岛C有多远?
(2)如果渔船继续向东航行,有无触礁危险?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求![]() 的长(结果保留π).
的长(结果保留π).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com