
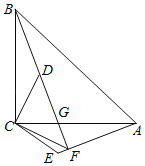
【题目】如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.
(1)求证:△ACE≌△BCD;
(2)求证:BF⊥AE;
(3)请判断∠CFE与∠CAB的大小关系并说明理由.
【答案】(1)见解析;(2)见解析;(3)∠CFE=∠CAB,见解析
【解析】
(1)根据垂直的定义得到∠ACB=∠DCE=90°,由角的和差得到∠BCD=∠ACE,即可得到结论;
(2)根据全等三角形的性质得到∠CBD=∠CAE,根据对顶角的性质得到∠BGC=∠AGE,由三角形的内角和即可得到结论;
(3)过C作CH⊥AE于H,CI⊥BF于I,根据全等三角形的性质得到AE=BD,S△ACE=S△BCD,根据三角形的面积公式得到CH=CI,于是得到CF平分∠BFH,推出△ABC是等腰直角三角形,即可得到结论.
(1)证明:∵BC⊥CA,DC⊥CE,
∴∠ACB=∠DCE=90°,
∴∠BCD=∠ACE,
在△BCD与△ACE中,
 ,
,
∴△ACE≌△BCD;
(2)∵△BCD≌△ACE,
∴∠CBD=∠CAE,
∵∠BGC=∠AGE,
∴∠AFB=∠ACB=90°,
∴BF⊥AE;
(3)∠CFE=∠CAB,
过C作CH⊥AE于H,CI⊥BF于I,
∵△BCD≌△ACE,
∴![]() ,
,
∴CH=CI,
∴CF平分∠BFH,
∵BF⊥AE,
∴∠BFH=90°,∠CFE=45°,
∵BC⊥CA,BC=CA,
∴△ABC是等腰直角三角形,
∴∠CAB=45°,
∴∠CFE=∠CAB.



 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】“知识改变命运,科技繁荣祖国.”为提升中小学生的科技素养,我区每年都要举办中小学科技节.为迎接比赛,该校在集训后进行了校内选拔赛,最后一轮复赛,决定在甲、乙2名候选人中选出1人代表学校参加区科技节项目的比赛,每人进行了4次测试,对照一定的标准,得分如下:甲:80,70,100,50;乙:75,80,75,70.如果你是教练,你打算安排谁代表学校参赛?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
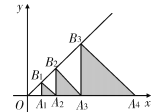
【题目】如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,OA1=1,且△B1A1A2,△B2A2A3,△B3A3A4,…△Bn A n A n+1…分别是以A1,A2,A3,…An…为直角顶点的等腰直角三角形,则△B10A10A11的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
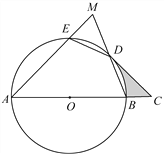
【题目】如图,AB是⊙O的直径,![]() ,连接ED,BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
,连接ED,BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
(1)若OA=CD=2![]() ,求阴影部分的面积;
,求阴影部分的面积;
(2)求证:DE=DM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=75°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D.则∠D的度数为( )

A.15°B.17.5°C.20°D.22.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A、B两城市相距100km.现计划在这两座城市间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上.已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内.请问计划修筑的这条高速公路会不会穿越保护区.为什么?(参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
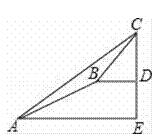
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,求大树CD的高度?(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数 y=kx+b 的图象经过点(-1,-5),且与正比例函数![]() 于点(2,a),求:
于点(2,a),求:
(1)a 的值;
(2)k,b 的值;
(3)这两个函数图象与 x 轴所围成的三角形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com