
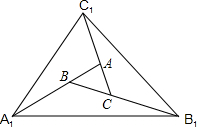
 如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=AB,B1C=BC,C1A=CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1,B1C1,C1A1至A2,B2,C2,使得A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,记其面积为S2…,按此规律继续下去.第n次操作得到△AnBnCn,则S1=7,△AnBnCn的面积Sn=7n.
如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=AB,B1C=BC,C1A=CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1,B1C1,C1A1至A2,B2,C2,使得A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,记其面积为S2…,按此规律继续下去.第n次操作得到△AnBnCn,则S1=7,△AnBnCn的面积Sn=7n. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>b,则ac2>bc2 | B. | 当x<7时,3(x-7)是负数 | ||
| C. | 若-$\frac{x}{3}$<0,则x>-3 | D. | 当x<0时,x2<3x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD的边长为6,点O是对角线AC,BD的交点,点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足为点F,连接OF.求:
如图,正方形ABCD的边长为6,点O是对角线AC,BD的交点,点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足为点F,连接OF.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图(1),四边形ABCD是一张边长为2a的正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线CG折叠,使点B落在EF上,对应点为B′.
如图(1),四边形ABCD是一张边长为2a的正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线CG折叠,使点B落在EF上,对应点为B′.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 旋转对称图形都是中心对称图形 | |
| B. | 角的对称轴就是它的角平分线 | |
| C. | 直角三角形三条高的交点就是它的直角顶点 | |
| D. | 钝角三角形的三条高(或所在直线)的交点在三角形的内部 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com