练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，点A、O、B在一条直线上，OF是∠AOE的平分线，OD是∠BOE的平分线．若∠DOB=28°，求∠EOF的度数．

    【答案】62°

    【解析】

    先根据∠DOB+∠AOD=180°求出∠AOD的度数,再根据角平分线的性质求出∠BOE的度数,由平角的性质可求出∠AOE的度数,OF是∠AOE的平分线即可求出∠EOF的度数.

    ∵∠DOB+∠AOD=180°, ∠DOB=28°,
    ∴∠AOD=152°;
    ∵OD是∠BOE的平分线,∠DOB=28°,
    ∴∠BOE=2∠BOD=2×28°=56°,
    ∴∠AOE=180°-∠BOE=180°-56°=124°,
    ∵OF是∠AOE的平分线,
    ∴∠EOF=∠AOE=×124°=62°.
    故答案为:62°.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线l1：分别与x轴、y轴交于点B、C，且与直线l2：交于点A．

    （1）求出点A的坐标

    （2）若D是线段OA上的点，且△COD的面积为12，求直线CD的解析式

    （3）在（2）的条件下，设P是射线CD上的点，在平面内是否存在点Q，使以O、C、P、Q为顶点的四边形是菱形？若存在，直接写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形ABCD中，E，F，G，H分别是边AB，DC，BC，AD上的点，且AE＝CF，BG＝DH.求证：EF与GH互相平分.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】常数a，b，c在数轴上的位置如图所示，则关于x的一元二次方程ax2+bx+c=0根的情况是（ ）
    A.有两个相等的实数根
    B.有两个不相等的实数根
    C.无实数根
    D.无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，函数y=2x和y=﹣x的图象分别为直线l1 ， l2 ， 过点（1，0）作x轴的垂线交l1于点A1 ， 过点A1作y轴的垂线交l2于点A2 ， 过点A2作x轴的垂线交l1于点A3 ， 过点A3作y轴的垂线交l2于点A4 ， …依次进行下去，则点A2017的坐标为 ．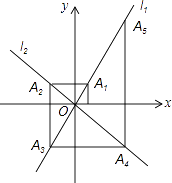

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果∠α和∠β互补，且∠α＞∠β，则下列表示∠β的余角的式子中：①90°﹣∠β；②∠α﹣90°③（∠α+∠β）；④（∠α﹣∠β）．正确的有（　　）

    A. 4个 B. 3个 C. 2个 D. 1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】边长为1的小正方形网格中，点A，B，C均落在格点上．

    （1）猜想△ABC的形状　 　，并证明；

    （2）直接写出△ABC的面积=　 　；

    （3）画出△ABC关于直线l的轴对称图形△A1B1C1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，点M为锐角三角形ABC内任意一点，连接AM、BM、CM．以AB为一边向外作等边三角形△ABE，将BM绕点B逆时针旋转60°得到BN，连接EN．

    （1）求证：△AMB≌△ENB；

    （2）若AM+BM+CM的值最小，则称点M为△ABC的费马点．若点M为△ABC的费马点，试求此时∠AMB、∠BMC、∠CMA的度数；

    （3）小翔受以上启发，得到一个作锐角三角形费马点的简便方法：如图②，分别以△ABC的AB、AC为一边向外作等边△ABE和等边△ACF，连接CE、BF，设交点为M，则点M即为△ABC的费马点．试说明这种作法的依据．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某剧院舞台上的照明灯P射出的光线成“锥体”，其“锥体”面图的“锥角”是60°．已知舞台ABCD是边长为6m的正方形．要使灯光能照射到整个舞台，则灯P的悬挂高度是（　　）

    A.3m
    B.3m
    C.4m
    D.m

    查看答案和解析>>

    同步练习册答案