
 如图,某水库大坝的横断面是梯形ABCD,坝顶宽CD=3m,坡角A为30°,坝高DE=8m,坝底宽AB为(27+8$\sqrt{3}$)m,试求迎水坡BC的长和迎水坡BC的坡度.
如图,某水库大坝的横断面是梯形ABCD,坝顶宽CD=3m,坡角A为30°,坝高DE=8m,坝底宽AB为(27+8$\sqrt{3}$)m,试求迎水坡BC的长和迎水坡BC的坡度. 分析 由题意得EF=DC=3m、DE=CF=8m,从而求得AE=$\frac{DE}{tanA}$=8$\sqrt{3}$,继而知BF=AB-AE-EF=24,再根据勾股定理和坡比的定义可得答案.
解答 解:根据题意知EF=DC=3,DE=CF=8,
∵在Rt△ADE中,AE=$\frac{DE}{tanA}$=$\frac{8}{\frac{\sqrt{3}}{3}}$=8$\sqrt{3}$,
∴BF=AB-AE-EF=27+8$\sqrt{3}$-8$\sqrt{3}$-3=24,
∴在Rt△BCF中,BC=$\sqrt{B{F}^{2}+C{F}^{2}}$=$\sqrt{2{4}^{2}+{8}^{2}}$=8$\sqrt{10}$(m),
迎水坡BC的坡度i=$\frac{CF}{BF}$=$\frac{8}{24}$=$\frac{1}{3}$.
点评 本题主要考查解直角三角形的应用-坡度、坡角问题,在解决坡度的有关问题中,一般通过作高构成直角三角形,坡角即是一锐角,坡度实际就是一锐角的正切值,水平宽度或铅直高度都是直角边,实质也是解直角三角形问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
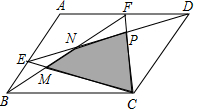 如图所示,在平行四边形ABCD中,E、F分别为AB和AD上的两个动点.
如图所示,在平行四边形ABCD中,E、F分别为AB和AD上的两个动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平行四边形ABCD中,点E为AD的中点,连CE,点M、N为CE上两点,且BM∥DN.
如图,平行四边形ABCD中,点E为AD的中点,连CE,点M、N为CE上两点,且BM∥DN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
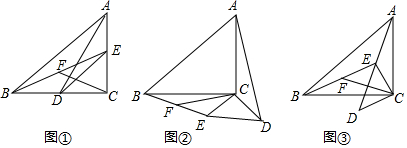
 如图,Rt△ABC中,∠C=90°,tanB=$\frac{1}{4}$,AD是BC边上的中线,则sin∠BAD=$\frac{2\sqrt{85}}{85}$.
如图,Rt△ABC中,∠C=90°,tanB=$\frac{1}{4}$,AD是BC边上的中线,则sin∠BAD=$\frac{2\sqrt{85}}{85}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com