
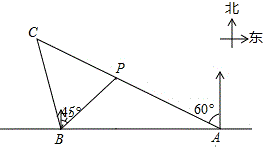
 如图,在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=8$\sqrt{6}$km,有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向,求点C与点B之间的距离(结果保留根号).
如图,在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=8$\sqrt{6}$km,有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向,求点C与点B之间的距离(结果保留根号). 分析 过点B作BF⊥AC于点F.求出各角的度数,在Rt△BCF中,利用三角函数的知识解答.
解答 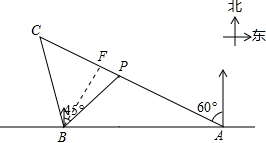 解:如图,过点B作BF⊥AC于点F.
解:如图,过点B作BF⊥AC于点F.
根据题意得:∠ABC=105°,∠BAF=30°
在Rt△ABF中,∠AFB=90°,∠BAF=30°
∴BF=$\frac{1}{2}$AB=4$\sqrt{6}$km.
在△ABC中,∠C=180°-∠BAC-∠ABC=45°,
在Rt△BCF中,∠BFC=90°,∠C=45°,
∴BC=$\sqrt{2}$BF=$8\sqrt{3}$km,
∴点C与点B之间的距离为$8\sqrt{3}$km.
点评 本题考查了解直角三角形的应用--做出辅助线,构造直角三角形是解题的关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
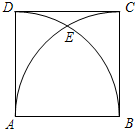 如图,正方形ABCD的边长AB=4,分别以点A、B为圆心,AB长为半径画弧,两弧交于点E,则CE弧的长是( )
如图,正方形ABCD的边长AB=4,分别以点A、B为圆心,AB长为半径画弧,两弧交于点E,则CE弧的长是( )| A. | $\frac{2}{3}π$ | B. | π | C. | $\frac{4}{3}π$ | D. | $\frac{8}{3}π$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
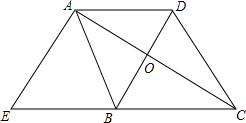 已知,如图,BD垂直平分AC,AE⊥AC,交CB的延长线于E,∠ABE=∠DCB.
已知,如图,BD垂直平分AC,AE⊥AC,交CB的延长线于E,∠ABE=∠DCB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径,BD平分∠CBQ交⊙O于点D,过点D作DE⊥PQ,垂足为E.
如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径,BD平分∠CBQ交⊙O于点D,过点D作DE⊥PQ,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com