
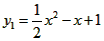 ,点F(1,1)。
,点F(1,1)。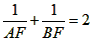 ;
; 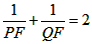 是否成立?请说明理由;
是否成立?请说明理由; 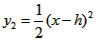 ,若2<x≤m时,y2≤x,恒成立,求m的最大值。
,若2<x≤m时,y2≤x,恒成立,求m的最大值。 解 (I)∵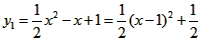 , ,∴抛物线 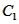 的顶点坐标为( 的顶点坐标为(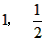 ); ); |
|
| (II)①根据题意,可得点A(0,1), ∵F(1,1), ∴AB∥x轴, 得AF=BF=1, 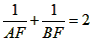 ; ;② 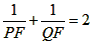 成立, 成立,理由如下: 如图,过点P( 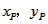 )作PM⊥AB于点M,则FM= )作PM⊥AB于点M,则FM=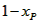 ,PM= ,PM=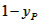 ( (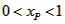 ) ) ∴Rt△PMF中,由勾股定理,得 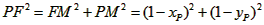 又点P( 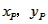 )在抛物线 )在抛物线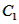 上, 上,得 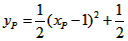 ,即 ,即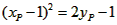 ∴ 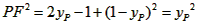 即 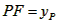 , ,过点Q( 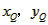 )作QN⊥B,与AB的延长线交于点N, )作QN⊥B,与AB的延长线交于点N,同理可得 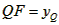 , ,图文∠PMF=∠QNF=90°,∠MFP=∠NFQ, ∴△PMF∽△QNF 有 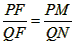 这里 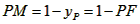 , ,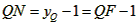 ∴ 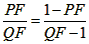 即 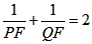 ; ; |
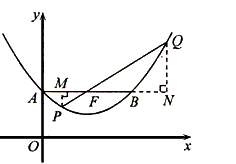 |
(Ⅲ)令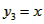 , ,设其图象与抛物线 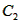 交点的横坐标为 交点的横坐标为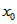 , ,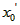 , ,且 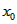 < <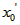 , , ∵抛物线 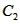 可以看作是抛物线 可以看作是抛物线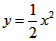 左右平移得到的, 左右平移得到的,观察图象,随着抛物线 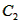 向右不断平移, 向右不断平移,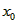 , ,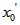 的值不断增大, 的值不断增大, ∴当满足 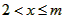 , ,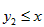 ,恒成立时,m的最大值在 ,恒成立时,m的最大值在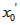 处取得, 处取得,可得当 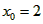 时, 时,所对应的 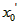 即为m的最大值, 即为m的最大值,于是,将 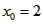 带入 带入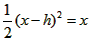 , ,有 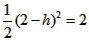 解得h=4或h=0(舍) ∴ 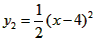 此时, 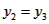 , ,得 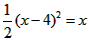 解得 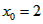 , ,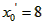 ∴m的最大值为8。 |


 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
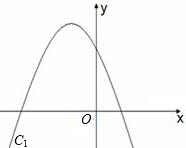 已知抛物线C1与x轴的一个交点为交于(-4,0),对称轴为x=-1.5,并过点(-1,6),
已知抛物线C1与x轴的一个交点为交于(-4,0),对称轴为x=-1.5,并过点(-1,6),查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011年天津市初中毕业生学业考试数学试卷 题型:044
已知抛物线C1:![]() .点F(1,1).
.点F(1,1).
(Ⅰ)求抛物线C1的顶点坐标;
(Ⅱ)①若抛物线C1与y轴的交点为A.连接AF,并延长交抛物线C1于点B,求证:![]()
②抛物线C1上任意一点P(xp,yp))(0<xp<1).连接PF.并延长交抛物线C1于点Q(xQ,yQ),试判断![]() 是否成立?请说明理由;
是否成立?请说明理由;
(Ⅲ)将抛物线C1作适当的平移.得抛物线C2:![]() ,若2<x≤m时.y2≤x恒成立,求m的最大值.
,若2<x≤m时.y2≤x恒成立,求m的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com