
分析 根据分式的性质,分子分母都乘以或除以同一个不为零的整式,分式的值不变,可得答案;
根据最简二次根式的两个条件:被开方数不含分母,被开方数不含开的尽的因数或因式,可得答案.
解答 解:$\frac{-21{x}^{3}{y}^{2}}{27{x}^{3}{y}^{3}{z}^{4}}$=$-\frac{7}{9y{z}^{4}}$(化成最简分式);$\sqrt{27{a}^{3}}$=3a$\sqrt{3a}$(化成最简二次根式),
故答案为:$-\frac{7}{9y{z}^{4}}$,3a$\sqrt{3a}$.
点评 本题考查了最简二次根式,最简二次根式的两个条件:被开方数不含分母,被开方数不含开的尽的因数或因式.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
| 年龄 | 28≤X<30 | 30≤X<32 | 32≤X<34 | 34≤X<36 | 36≤X<38 | 38≤X<40 | 40≤X<42 |
| 频数 | 4 | 3 | 8 | 7 | 9 | 11 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
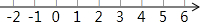 解不等式组$\left\{\begin{array}{l}3(x+1)≤9\\ x+5>4\end{array}\right.$,并将其解集表示在数轴上.
解不等式组$\left\{\begin{array}{l}3(x+1)≤9\\ x+5>4\end{array}\right.$,并将其解集表示在数轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
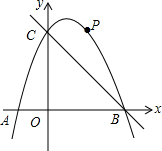 如图,在平面直角坐标系中,二次函数y=-x2+bx+c的图象与x轴交于A、B两点,与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0).点P是抛物线上一个动点,且在直线BC的上方.
如图,在平面直角坐标系中,二次函数y=-x2+bx+c的图象与x轴交于A、B两点,与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0).点P是抛物线上一个动点,且在直线BC的上方.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com