练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．已知不等式4x-a≤0的正整数解是1，2，则a的取值范围是（　　）
    A．8＜a＜12B．8≤a＜12C．8＜a≤12D．8≤a≤12

    分析 先求出不等式的解集，再根据整数解为1，2逆推a的取值范围．

    解答 解：不等式4x-a≤0的解集是x≤$\frac{a}{4}$，
    因为正整数解是1，2，
    而只有当不等式的解集为x≤2，x≤2.1，x≤2.2等时，但x＜3时，其整数解才为1，2，
    则2≤$\frac{a}{4}$＜3，
    即a的取值范围是8≤a＜12，
    故选B

    点评 此题考查不等式问题，解答此题要先求出不等式的解集，再根据整数解的情况确定a的取值范围．本题要求熟练掌握不等式及不等式的解法，准确的理解整数解在不等式解集中的意义，并会逆推式子中有关字母的取值范围．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．计算：$\sqrt{3}tan30°+（\frac{1}{2}{）^{-2}}+|{\sqrt{2}-1}|+\root{3}{-64}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

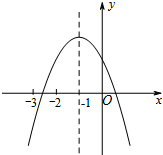    1．如图是二次函数y=ax2+bx+c图象的一部分，过点（x1，0），-3＜x1＜-2，对称轴为直线x=-1．给出四个结论：①abc＞0；②2a+b=0；③b2＞4ac；④3b+2c＞0，其中正确的结论有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．$\frac{-21{x}^{3}{y}^{2}}{27{x}^{3}{y}^{3}{z}^{4}}$=$-\frac{7}{9y{z}^{4}}$（化成最简分式）；$\sqrt{27{a}^{3}}$=3a$\sqrt{3a}$（化成最简二次根式）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．解方程组
    （1）$\left\{\begin{array}{l}{x-2y=4}\\{2x-y=6}\end{array}\right.$　　　　　　　
    （2）$\left\{\begin{array}{l}{\stackrel{x+y=8}{y+z=6}}\\{x+z=4}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

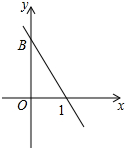    15．如图，在平面直角坐标系xOy中，直线$y=-\frac{3}{2}x+b$经过第一、二、四象限，与y轴交于点B，点A（2，m）在这条直线上，连结AO，△AOB的面积等于2．
    （1）求b的值；
    （2）如果反比例函数$y=\frac{k}{x}$（k是常量，k≠0）的图象经过点A，求这个反比例函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．在正方形ABCD中，点P是射线CB上一个动点，连接PA，PD，点M、N分别为BC、AP的中点，连接MN交PD于点Q．
    （1）如图1，当点P与点B重合时，△QPM的形状是等腰直角三角形；
    （2）当点P在线段CB的延长线上时，如图2．
    ①依题意补全图2；
    ②判断△QPM的形状并加以证明；
    （3）点P′于点P关于直线AB对称，且点P′在线段BC上，连接AP′，若点Q恰好在直线AP′上，正方形ABCD的边长为2，请写出求此时BP长的思路（可以不写出计算结果）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

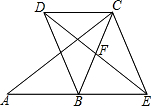    19．如图，在△ABC中，点F是BC的中点，点E是线段AB的延长线上的一动点，连接EF，过点C作AB的平行线CD，与线段EF的延长线交于点D，连接CE、BD．
    （1）求证：四边形DBEC是平行四边形．
    （2）若∠ABC=120°，AB=BC=4，则在点E的运动过程中：
    ①当BE=2时，四边形BECD是矩形，试说明理由；
    ②当BE=4时，四边形BECD是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．我们知道，在反比例函数y=$\frac{2}{x}$的图象上任取一点，过该点分别向两条坐标轴画垂线，这两条垂线与坐标轴围成的矩形面积始终是2．如果在某个函数的图象上任取一点，按同样的方式得到的矩形的周长始终是2，这个函数是y=-x+1（0＜x＜1）．（写出一个满足条件的函数表达式及自变量的取值范围）

    查看答案和解析>>

    同步练习册答案