
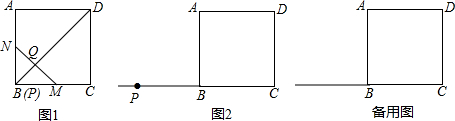
���� ��1������AC���������ε����ʵõ���DBC=45�㣬�������BQM=90�㣬���ݵ���ֱ�������ε��ж����ɽ��
��2���ٸ������ⲹ��ͼ�μ��ɣ�
�ڡ�QPM����״�ǵ��������Σ��ӳ�BC��E��ʹCE=BP������AE��֤����DCP�ա�ABE���õ���DPC=��E����֤��MN��AE���õ���NMP=��E��ͨ�����������õ���DPC=��NMP�����ݵȽǶԵȱߵõ�QM=QP�����ɽ��
��3���������������ε����ʶ������ж��������ԳƵ����ʣ�д������˼·��
��� �⣺��1����ͼ1������AC��
���ı���ABCDΪ�����Σ�
��AC��BD����DBC=45�㣬
�ߵ�M��N�ֱ�ΪBC��AP���е㣬
��MN��AC��
���BQM=��BOC=90�㣬
���QMB=45�㣬
���QPM�ǵ���ֱ�������Σ�
�ʴ�Ϊ������ֱ�������Σ�
��2������ͼ2��
�ڡ�QPM����״�ǵ��������Σ�
��ͼ3���ӳ�BC��E��ʹCE=BP������AE��
��PB=CE��
��PB+BC=CE+BC����CP=BE��
���ı���ABCD�������Σ�
��AB=DC����ABC=��DCB=90�㣬
�ڡ�DCP�͡�ABE�У�
$\left\{\begin{array}{l}{DC=AB}\\{��DCP=��ABE}\\{CP=BE}\end{array}\right.$
���DCP�ա�ABE��
���DPC=��E��
��MΪBC���е㣬
��MB=MC��
��MB+BP=MC+CE����MP=ME��
��MΪPE���е㣬
��NΪAP���е㣬
��MN��AE��
���NMP=��E��
���DPC=��NMP��
��QM=QP��
���QPM�ǵ��������Σ�
��3�����˼·���£�
a�������⻭��ͼ�Σ����ӳ�BC��E��ʹCE=BP������AE����ͼ4��
b���ɣ�2���ɵ�QM��AE����֤$\frac{P��Q}{QA}=\frac{P��M}{ME}$��
c����PP���AD����֤��P��PQ�ס�ADQ���Ӷ�$\frac{P��Q}{QA}=\frac{P��P}{AD}$��
d���ɵ�$\frac{P��M}{ME}=\frac{P��P}{AD}$��
e���ɵ�P�����P����ֱ��AB�Գƣ��õ�BP��=BP=CE����BP��=BP=CE=x����AD=BC=2���ɷֱ��ʾP��M��ME��P��P������BP�ij���
���� ���⿼���������ε����ʡ�����ֱ�������ε��ж������������ε����ʶ������ж�������ȫ�������ε����ʶ������ж��������������Ĺؼ������������ߣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8��a��12 | B�� | 8��a��12 | C�� | 8��a��12 | D�� | 8��a��12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
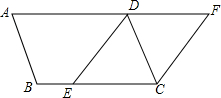 ��ͼ��?ABCD����E��BC�ߵ�һ�㣬����AD�ӳ�����F��ʹ��AFC=��DEC������CF��DE��
��ͼ��?ABCD����E��BC�ߵ�һ�㣬����AD�ӳ�����F��ʹ��AFC=��DEC������CF��DE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
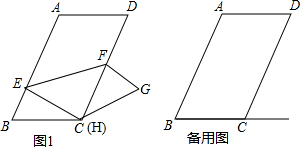
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com