
分析 (1)根据加减消元法消去x,可以得到y的值,再将y的值代入原方程组即可求得x的值,本题得以解决;
(2)根据加减消元法,将原方程组变为二元,然后再变为一元一次方程,本题得以解决.
解答 解:(1)$\left\{\begin{array}{l}{x-2y=4}&{①}\\{2x-y=6}&{②}\end{array}\right.$
①×2-②,得
-3y=2
解得,y=$-\frac{2}{3}$,
将y=-$\frac{2}{3}$代入①,得
x=$\frac{8}{3}$
故原方程组的解是$\left\{\begin{array}{l}{x=\frac{8}{3}}\\{y=-\frac{2}{3}}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x+y=8}&{①}\\{y+z=6}&{②}\\{x+z=4}&{③}\end{array}\right.$
①-②,得
x-z=2④
③+④,得
x=3
将x=3代入①,得
y=5,
将x=3代入③,得
z=1
故原方程组的解是
$\left\{\begin{array}{l}{x=3}\\{y=5}\\{z=1}\end{array}\right.$.
点评 本题考查解二元一次方程组、解三元一次方程组,解题的关键是明确解方程组的方法,会用消元法解方程组.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
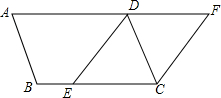 如图,?ABCD,点E是BC边的一点,将边AD延长至点F,使∠AFC=∠DEC,连接CF、DE.
如图,?ABCD,点E是BC边的一点,将边AD延长至点F,使∠AFC=∠DEC,连接CF、DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
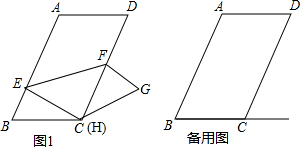
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com