
ЁОЬтФПЁПШчЭММзЃЌABЁЭBDЃЌCDЁЭBDЃЌAPЁЭPCЃЌДЙзуЗжБ№ЮЊBЁЂPЁЂDЃЌЧвШ§ИіДЙзудкЭЌвЛжБЯпЩЯЃЌЮвУЧАбетбљЕФЭМаЮНаЁАШ§ДЙЭМЁБЃЎ
ЃЈ1ЃЉжЄУїЃКABCD=PBPDЃЎ
ЃЈ2ЃЉШчЭМввЃЌвВЪЧвЛИіЁАШ§ДЙЭМЁБЃЌЩЯЪіНсТлГЩСЂТ№ЃПЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉвбжЊХзЮяЯпгыxжсНЛгкЕуAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌгыyжсНЛгкЕуЃЈ0ЃЌ-3ЃЉЃЌЖЅЕуЮЊPЃЌШчЭМБћЫљЪОЃЌШєQЪЧХзЮяЯпЩЯвьгкAЁЂBЁЂPЕФЕуЃЌЪЙЕУЁЯQAP=90ЁуЃЌЧѓQЕузјБъЃЎ

ЁОД№АИЁПЃЈ1ЃЉЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЭЌНЧЕФгрНЧЯрЕШЧѓГіЁЯA=ЁЯCPDЃЌШЛКѓЧѓГіЁїABPКЭЁїPCDЯрЫЦЃЌдйИљОнЯрЫЦШ§НЧаЮЖдгІБпГЩБШР§СаЪНећРэМДПЩЕУжЄЃЛ
ЃЈ2ЃЉгыЃЈ1ЃЉЕФжЄУїЫМТЗЯрЭЌЃЛ
ЃЈ3ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіЖўДЮКЏЪ§НтЮіЪНЃЌИљОнХзЮяЯпНтЮіЪНЧѓГіЕуPЕФзјБъЃЌдйЙ§ЕуPзїPCЁЭxжсгкCЃЌЩшAQгыyжсЯрНЛгкDЃЌШЛКѓЧѓГіPCЁЂACЕФГЄЃЌдйИљОнЃЈ2ЃЉЕФНсТлЧѓГіODЕФГЄЃЌДгЖјЕУЕНЕуDЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпADЕФНтЮіЪНЃЌгыХзЮяЯпНтЮіЪНСЊСЂЧѓНтМДПЩЕУЕНЕуQЕФзјБъЃЎ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉжЄУїЃКЁпABЁЭBDЃЌCDЁЭBDЃЌ
ЁрЁЯB=ЁЯD=90ЁуЃЌ
ЁрЁЯA+ЁЯAPB=90ЁуЃЌ
ЁпAPЁЭPCЃЌ
ЁрЁЯAPB+ЁЯCPD=90ЁуЃЌ
ЁрЁЯA=ЁЯCPDЃЌ
ЁрЁїABPЁзЁїPCDЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрABCD=PBPDЃЛ
ЃЈ2ЃЉABCD=PBPDШдШЛГЩСЂЃЎ
РэгЩШчЯТЃКЁпABЁЭBDЃЌCDЁЭBDЃЌ
ЁрЁЯB=ЁЯCDP=90ЁуЃЌ
ЁрЁЯA+ЁЯAPB=90ЁуЃЌ
ЁпAPЁЭPCЃЌ
ЁрЁЯAPB+ЁЯCPD=90ЁуЃЌ
ЁрЁЯA=ЁЯCPDЃЌ
ЁрЁїABPЁзЁїPCDЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрABCD=PBPDЃЛ
ЃЈ3ЃЉЩшХзЮяЯпНтЮіЪНЮЊ![]() ЃЈaЁй0ЃЉЃЌ
ЃЈaЁй0ЃЉЃЌ
ЁпХзЮяЯпгыxжсНЛгкЕуAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌгыyжсНЛгкЕуЃЈ0ЃЌ-3ЃЉЃЌ
Ёр![]() ЃЌ АбЃЈ0ЃЌ-3ЃЉДјШы
ЃЌ АбЃЈ0ЃЌ-3ЃЉДјШы
ЕУ y=x2-2x-3ЃЌ
Ёпy=x2-2x-3=ЃЈx-1ЃЉ2-4ЃЌ
ЁрЖЅЕуPЕФзјБъЮЊЃЈ1ЃЌ-4ЃЉЃЌ
Й§ЕуPзїPCЁЭxжсгкCЃЌЙ§ЕуQЯђxжсзїДЙЯпЃЌДЙзуЮЊE.
ЩшQE=mЃЌгЩЕк(2)ЬтНсТлЕУAE=2mЃЌдђQЕузјБъЮЊЃЈ2m -1ЃЌmЃЉДјШыy=x2-2x-3ЃЌ
НтЕУm=![]() Лђm=0ЃЈЩсШЅЃЉЃЌАбy=
Лђm=0ЃЈЩсШЅЃЉЃЌАбy=![]() ДјШыy=x2-2x-3ЃЌНтЕУx=
ДјШыy=x2-2x-3ЃЌНтЕУx=![]() Лђx=
Лђx=![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
ЁрЕуQЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉ
ЃЉ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁЯBAC=40ЁуЃЌАбЁїABCШЦзХЕуAЫГЪБеыа§зЊЃЌЪЙЕУЕуBгыCAЕФбгГЄЯпЩЯЕФЕуDжиКЯЃЎ
ЃЈ1ЃЉЁїABCа§зЊСЫЖрЩйЖШЃП
ЃЈ2ЃЉЧѓЁЯAECЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОЬтТњЗж10ЗжЃЉвбжЊЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() гаСНИіВЛЯрЕШЕФЪЕЪ§Иљ
гаСНИіВЛЯрЕШЕФЪЕЪ§Иљ![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЪдЫЕУї![]() ЃЌ
ЃЌ ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШєХзЮяЯп![]() гы
гы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЕу
СНЕуЃЌЕу![]() ЁЂЕу
ЁЂЕу![]() ЕНдЕуЕФОрРыЗжБ№ЮЊ
ЕНдЕуЕФОрРыЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ8ЗжЃЉШчЭМЃЌRtЁїABCжаЃЌAC=BC=2ЃЌе§ЗНаЮCDEFЕФЖЅЕуDЁЂFЗжБ№дкACЁЂBCБпЩЯЃЌCЁЂDСНЕуВЛжиКЯЃЌЩшCDЕФГЄЖШЮЊxЃЌЁїABCгые§ЗНаЮCDEFжиЕўВПЗжЕФУцЛ§ЮЊyЃЌ
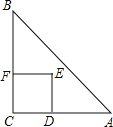
(1)ЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕ
(2)xЮЊКЮжЕЪБжиЕўВПЗжЕФУцЛ§зюДѓ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПAЁЂBСНЕуЕФзјБъЗжБ№ЮЊЃЈ1ЃЌ0ЃЉЁЂЃЈ0ЃЌ2ЃЉЃЌШєНЋЯпЖЮABЦНвЦжСA1B1ЃЌЕуA1B1ЕФзјБъЗжБ№ЮЊЃЈ2ЃЌaЃЉЁЂЃЈbЃЌ3ЃЉЃЌдђa+b=____________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЖўДЮКЏЪ§y=x2+ЃЈ2kЉ1ЃЉx+k+1ЕФЭМЯѓгыxжсЯрНЛгкOЁЂAСНЕуЃЎ
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкетЬѕХзЮяЯпЕФЖдГЦжсгвБпЕФЭМЯѓЩЯгавЛЕуBЃЌЪЙШёНЧЁїAOBЕФУцЛ§ЕШгк3ЃЎЧѓЕуBЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧЖўДЮКЏЪ§yЃНax2ЃЋbxЃЋcЭМЯѓЕФвЛВПЗжЃЌЭМЯѓЙ§ЕуA(Ѓ3ЃЌ0)ЃЌЖдГЦжсЮЊжБЯпxЃНЃ1ЃЌИјГівдЯТНсТлЃКЂйabc<0ЃЛЂкb2Ѓ4ac>0ЃЛЂл4bЃЋc<0ЃЛЂмШєB(Ѓ![]() ЃЌy1)ЃЌC(Ѓ
ЃЌy1)ЃЌC(Ѓ![]() ЃЌy2)ЮЊКЏЪ§ЭМЯѓЩЯЕФСНЕуЃЌдђy1>y2ЃЛЂнЕБЃ3ЁмxЁм1ЪБЃЌyЁн0ЃЌЦфжае§ШЗЕФНсТлЪЧ______ЃЎ(ЬюађКХ)
ЃЌy2)ЮЊКЏЪ§ЭМЯѓЩЯЕФСНЕуЃЌдђy1>y2ЃЛЂнЕБЃ3ЁмxЁм1ЪБЃЌyЁн0ЃЌЦфжае§ШЗЕФНсТлЪЧ______ЃЎ(ЬюађКХ)

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаГЄЖШЕФШ§ИљаЁФОАєФмЙЙГЩШ§НЧаЮЕФЪЧ
A. 2cm,3cm,5cmB. 2cm,4cm,7cmC. 3cm,3cm,4cmD. 3cm,4cm,8cm
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛДЮКЏЪ§y=kx+b ЕФЭМЯёгыЗДБШР§КЏЪ§y=Ѓ8/x ЕФЭМЯёНЛгкAЁЂBСНЕуЃЌЧвЕуAЕФКсзјБъКЭЕуBЕФзнзјБъЖМЪЧЃ2 ЃЌ ЧѓЃК
ЃЈ1ЃЉвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЁїAOBЕФУцЛ§
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com