
| A. | $\frac{7}{2}$ | B. | 3 | C. | $\frac{5}{2}$ | D. | 2 |
分析 过A作PQ∥BC交BF的延长线于Q,交CE的延长线于P,根据全等三角形的性质得到$\frac{AF}{CF}=\frac{AQ}{BC},\frac{AE}{BE}=\frac{AP}{BC}$,根据比例的性质得到$\frac{AF+CF}{CF}=\frac{AQ+BC}{BC}$,$\frac{AE+BE}{BE}=\frac{AP+BC}{BC}$,两式相加得到$\frac{PQ+2BC}{BC}=5$,即可得到结论.
解答 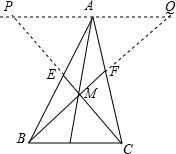 解:过A作PQ∥BC交BF的延长线于Q,交CE的延长线于P,
解:过A作PQ∥BC交BF的延长线于Q,交CE的延长线于P,
∴△AQF∽△BCF△APE∽△BCE,
∴$\frac{AF}{CF}=\frac{AQ}{BC},\frac{AE}{BE}=\frac{AP}{BC}$,
∴$\frac{AF+CF}{CF}=\frac{AQ+BC}{BC}$,$\frac{AE+BE}{BE}=\frac{AP+BC}{BC}$,
即$\frac{AC}{CF}=\frac{AQ+BC}{BC}$,$\frac{AB}{BE}=\frac{AP+BC}{BC}$,
∵$\frac{AC}{CF}+\frac{AB}{BE}=\frac{AQ+BC+AP+BC}{BC}=5$,
∴$\frac{PQ+2BC}{BC}=5$,
∴$\frac{AM}{MD}=\frac{QM}{BM}=\frac{PQ}{BC}$=3.
故选B.
点评 本题考查了相似三角形的判定和性质,比例的性质,正确的作出辅助线是解题的关键.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:选择题
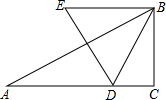 如图,已知△ABC,∠C=90°,∠A=30°,AC=$\sqrt{3}$,动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧),在点D从点A移动至点C的过程中,点E移动的路线为( )
如图,已知△ABC,∠C=90°,∠A=30°,AC=$\sqrt{3}$,动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧),在点D从点A移动至点C的过程中,点E移动的路线为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图所示,在?ABCD中,∠BAD的平分线与BC交于E,∠ABC的平分线交AD于点F,AE,BF交于O,则四边形ABEF为菱形,请说明理由.
已知,如图所示,在?ABCD中,∠BAD的平分线与BC交于E,∠ABC的平分线交AD于点F,AE,BF交于O,则四边形ABEF为菱形,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
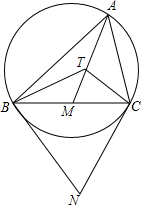 已知锐角△ABC及其外接圆,AM是边BC的中线,分别过点B,C作外接圆的切线,两条切线交于点N,T是AM上的一点,且∠ATC=∠ABN,求证:$\frac{AB}{AC}=\frac{TB}{TC}$.
已知锐角△ABC及其外接圆,AM是边BC的中线,分别过点B,C作外接圆的切线,两条切线交于点N,T是AM上的一点,且∠ATC=∠ABN,求证:$\frac{AB}{AC}=\frac{TB}{TC}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某移动公司近日推出了如下两种月收费方式.
某移动公司近日推出了如下两种月收费方式.| 收费方式 | 月租费/元 | 赠送通话时间/分钟 | 超时费/(元/分钟) |
| A | k | l | 0.2 |
| B | m | n | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
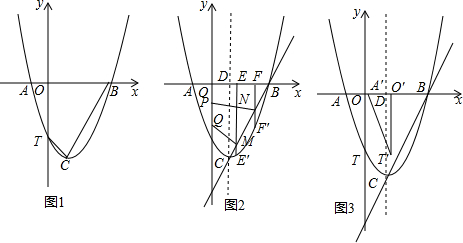
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<$\frac{1}{3}$ | B. | m<-$\frac{1}{3}$ | C. | m>$\frac{1}{3}$ | D. | m>-$\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com